题目内容
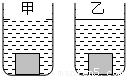 将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是 .(g取10N/kg)
将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是 .(g取10N/kg)
【答案】分析:已知水对容器底部增加的压强,根据公式P=ρgh可求水增加的深度,根据公式V=Sh求出水上升的体积;也就是金属块的体积;进一步求出甲内液体的密度,根据浮力公式求出金属块在甲中受到的浮力,根据二力平衡求出金属块的重力,进一步求出金属块的质量,根据密度公式求出金属块的密度.
解答:解:水增加的深度h=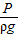 =
=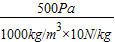 =0.05m;
=0.05m;
金属块的体积V=Sh=0.05m×100×10-4m2=5×10-4m3;
甲内液体的密度ρ液=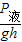 =
=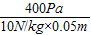 =800kg/m3;
=800kg/m3;
金属块受到的浮力F浮=ρ液gV=800kg/m3×10N/kg×5×10-4m3=4N;
金属块的重力G=F浮+N=4N+26N=30N;
金属块的质量m=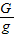 =
=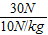 =3kg;
=3kg;
金属块的密度ρ金=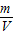 =
=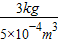 =6×103kg/m3.
=6×103kg/m3.
故答案为:6×103kg/m3.
点评:本题考查压力、压强、深度、体积、密度的计算,关键是公式及其变形的灵活运用,难点是求金属块的密度,解题过程中要注意单位的换算.
解答:解:水增加的深度h=
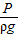 =
=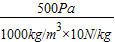 =0.05m;
=0.05m;金属块的体积V=Sh=0.05m×100×10-4m2=5×10-4m3;
甲内液体的密度ρ液=
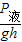 =
=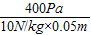 =800kg/m3;
=800kg/m3;金属块受到的浮力F浮=ρ液gV=800kg/m3×10N/kg×5×10-4m3=4N;
金属块的重力G=F浮+N=4N+26N=30N;
金属块的质量m=
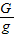 =
=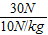 =3kg;
=3kg;金属块的密度ρ金=
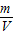 =
=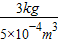 =6×103kg/m3.
=6×103kg/m3.故答案为:6×103kg/m3.
点评:本题考查压力、压强、深度、体积、密度的计算,关键是公式及其变形的灵活运用,难点是求金属块的密度,解题过程中要注意单位的换算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
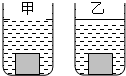 将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是
将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是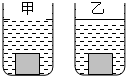 将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是________.(g取10N/kg)
将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是________.(g取10N/kg) 将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是 .(g取10N/kg)
将底面积均为100cm2的甲、乙两个圆柱形玻璃杯放在水平桌面上,如图所示.甲玻璃杯中装有未知密度的液体,乙玻璃杯中装有水.将一金属块没入甲杯液体中时,液体对杯底的压强比没放入金属块时增加了400pa,容器底对金属块的支持力为26N.将该金属块没入乙杯的水中时,水对杯底的压强比没放入金属块时增加了500Pa(两杯中的液体均未溢出).则金属块的密度是 .(g取10N/kg)