题目内容
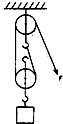 如图所示,用滑轮组匀速提起一个重为350N的物体,物体在10s内竖直上升了1m,人拉绳的力为250N.不计绳重和摩擦,试问:
如图所示,用滑轮组匀速提起一个重为350N的物体,物体在10s内竖直上升了1m,人拉绳的力为250N.不计绳重和摩擦,试问:(1)人做的有用功
(2)滑轮组的机械效率为多少?
(3)动滑轮重多少?
(4)若用这个滑轮组将650N的重物提升1m,拉力做了多少功?此时的机械效率与第(2)问相比如何变化?
分析:(1)利用功的计算公式W有用=Gh即可求出有用功;
(2)利用η=
=
=
即可求出机械效率;
(3)使用滑轮组不计绳重和摩擦时,则F=
(G+G动),由此即可求出动滑轮重;
(4)根据F=
(G+G动)求出拉力大小,利用W总=Fs求出拉力做的功;用η=
即可求出机械效率;然后比较.
(2)利用η=
| W有用 |
| W总 |
| Gh |
| Fs |
| Gh |
| F?nh |
| G |
| nF |
(3)使用滑轮组不计绳重和摩擦时,则F=
| 1 |
| n |
(4)根据F=
| 1 |
| n |
| G |
| nF |
解答:解:(1)W有用=Gh=350N×1m=350J;
(2)∵η=
=
=
=
,
∴η=
×100%=
×100%=70%;
(3)不计绳重和摩擦时,则F=
(G+G动),
∴G动=2F-G=2×250N-350N=150N;
(4)∵F2=
(G′+G动),
∴F2=
(G′+G动)=
×(650N+150N)=400N;
∴W总2=F2×s2=400N×1m×2=800J;
∵η′=
×100%=
×100%=81.25%.
∴此时的机械效率与第(2)问相比增大.
答:(1)人做的有用功是350J,
(2)滑轮组的机械效率为70%;
(3)动滑轮重为150N;
(4)若用这个滑轮组将650N的重物提升1m,拉力做了800J的功;此时的机械效率与第(2)问相比增大.
(2)∵η=
| W有用 |
| W总 |
| Gh |
| Fs |
| Gh |
| F?nh |
| G |
| nF |
∴η=
| G |
| nF |
| 350N |
| 2×250N |
(3)不计绳重和摩擦时,则F=
| 1 |
| 2 |
∴G动=2F-G=2×250N-350N=150N;
(4)∵F2=
| 1 |
| 2 |
∴F2=
| 1 |
| 2 |
| 1 |
| 2 |
∴W总2=F2×s2=400N×1m×2=800J;
∵η′=
| G′ |
| nF2 |
| 650N |
| 2×400N |
∴此时的机械效率与第(2)问相比增大.
答:(1)人做的有用功是350J,
(2)滑轮组的机械效率为70%;
(3)动滑轮重为150N;
(4)若用这个滑轮组将650N的重物提升1m,拉力做了800J的功;此时的机械效率与第(2)问相比增大.
点评:本题的难度较大,要求对功、功率以及机械效率的计算熟练掌握,并能灵活应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 小悦用如图所示的滑轮组,在10s钟内将重力为600N的物体A匀遭提升了2m.巳知绳子自由端所用的拉力为200N.(不计摩擦及绳重)
小悦用如图所示的滑轮组,在10s钟内将重力为600N的物体A匀遭提升了2m.巳知绳子自由端所用的拉力为200N.(不计摩擦及绳重) (2011?南充)如图所示,某建筑工地用电动机和滑轮组把建筑材料从地面提升到工作平台上.已知建筑材料的质量m=360kg,用t=20s的时间把建筑材料匀逮提升了h=4m,滑轮组的机械效率为90%,g取10N/Kg.求这段时间内
(2011?南充)如图所示,某建筑工地用电动机和滑轮组把建筑材料从地面提升到工作平台上.已知建筑材料的质量m=360kg,用t=20s的时间把建筑材料匀逮提升了h=4m,滑轮组的机械效率为90%,g取10N/Kg.求这段时间内 建筑工地上,工人用如图所示的装置将重为500N的建材从地面匀速送到6m高处,所用拉力为300N,时间为20s.不计摩擦和绳重,求:
建筑工地上,工人用如图所示的装置将重为500N的建材从地面匀速送到6m高处,所用拉力为300N,时间为20s.不计摩擦和绳重,求: 雅安地震后重建家园的某工地上,工人用如图所示的装置将重为200N的建材从地面匀速送到6m高处,所用拉力为125N,时间为10s.求:
雅安地震后重建家园的某工地上,工人用如图所示的装置将重为200N的建材从地面匀速送到6m高处,所用拉力为125N,时间为10s.求: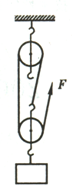 如图所示,某人用滑轮组匀逮提升重120N的物体,人的拉力为50N,在2s内,绳的自由端移动了6米:
如图所示,某人用滑轮组匀逮提升重120N的物体,人的拉力为50N,在2s内,绳的自由端移动了6米: