Question

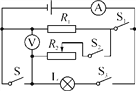
【题目】如图，电源电压恒定，灯L的规格为“24 V 72 W”且工作时电阻保持不变，电压表的量程为0～15 V，电流表的量程为0～3 A，在电路安全的前提下，操作如下：当只闭合S、S3时，电路中的总功率为P1，电流表示数为I1；当只闭合S2、S3时，移动滑片使滑动变阻器的阻值为R，电流表示数为I2，电阻R1和滑动变阻器的总功率为10 W；再移动滑片使滑动变阻器的阻值为2R，电流表示数为I3，灯L和滑动变阻器的总功率为9.72 W；当只闭合S、S1、S2时，移动滑动变阻器的滑片，使电路中的最小总功率为P4，此时电流表示数为I4。已知P1∶P4＝5∶6，I2∶I3＝10∶9，则I1∶I4＝_______，当滑动变阻器R2的阻值为______Ω时，该电路消耗的功率为最小。

Answer 1

【答案】 5∶6 32

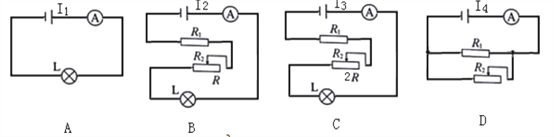
【解析】当只闭合S、S3时，只有灯泡连入电路，如图A所示；当只闭合S2、S3时，电阻R1、滑动变阻器和灯泡串联，滑动变阻器的阻值为R，如图所示B；再移动滑片使滑动变阻器的阻值为2R，如图C所示；当只闭合S、S1、S2时，电阻R1、滑动变阻器并联，如图D所示：

（1）由P＝得：灯泡的电阻RL＝＝8Ω；（2）由图AD可知：电源电压不变，由P＝UI得：；（3）由图B可知：R总2＝R1RRL，由图C可知：R总3＝R1+2R+RL，则I2＝，I3＝，已知：I2:I3＝10:9，则:＝10:9；即：R1＝8RRL＝8R-8Ω①,由P＝I2R得：图B中电阻R1和滑动变阻器的总功率P′＝(R1R)，即 (R1R)＝10W②,图C中灯泡和滑动变阻器的总功率P″＝(RL2R)，即 (8Ω2R)＝9.72W③,由于I2:I3＝10:9，则得：3R1＝20Ω2R④,解①④方程得：R1＝8Ω，R＝2Ω，由②得：I2＝ ＝＝1A，根据图B可知：电源电压U＝I2(R1RRL)＝1A×(8Ω2Ω8Ω)＝18V，由电路图可知：该电路消耗的功率最小是只闭合S2、S3，R1、灯泡和滑动变阻器串联，由于此时电压表测量R1和滑动变阻器两端的电压，则电压表示数U′为最大15V时，电路中的电阻最大，电流最小，此时的功率最小；根据串联电路的总电压等于各电阻两端的电压之和可知：灯泡两端的电压UL＝UU′＝18V15V＝3V；此时电路中的电流I′＝IL＝＝0.375A，由I＝得此时电路的最小电阻为R最小＝＝48Ω，根据串联电路的总电阻等于各分电阻之和可知：滑动变阻器连入电路的最大阻值为：R滑＝R最小R1RL＝48Ω8Ω8Ω＝32Ω。