Question

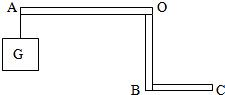如图所示，曲杆AOBC自重不计，O为支点，AO=60cm，OB=40cm，BC=30cm，A端所挂重物G=50N，为使杠杆在图示位置平衡，需在C处施加一个力．
①为使用力最小，这个力的方向如何？试在图上画出该力的示意图；
②计算该力的大小．

Answer 1

分析：根据杠杆平衡的条件，F₁×L₁=F₂×L₂，在杠杆中的阻力、阻力臂一定的情况下，要使所用的动力最小，必须使动力臂最长．而在通常情况下，连接杠杆中支点和动力作用点这两点所得到的线段最长，利用题目中所知数据可计算出力的大小．

解答：解：①连接OC就是最长的动力臂，根据杠杆平衡的条件，要使杠杆平衡动力方向向下，据此可画出最小的动力；如图：

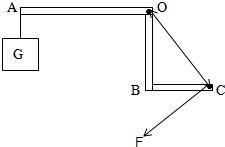
②OC=

OB2+BC2

=

(40cm)2+(30cm)2

=50cm，拉力F=

G×AO

OC

=

50N×60cm

50cm

=60N
答：该力的大小是60N．

点评：要做出杠杆中的最小动力，可以按照以下几个步骤进行：
1、确定杠杆中的支点和动力作用点的位置；
2、连接支点与动力作用点，得到最长的线段；
3、经过动力作用点做出与该线段垂直的直线；
4、根据杠杆平衡原理，确定出使杠杆平衡的动力方向．