题目内容
（2009?怀柔区一模）在如图所示的电路中，灯泡L标有“6V 3W”字样，电源两端的电压和灯丝的电阻均保持不变．当开关S1、S2都断开时，滑动变阻器R的滑片P从b端滑到某一位置c时（图中未标出），滑动变阻器R接入电路的电阻减小6Ω，电流表示数变化了0.1 A，灯泡恰好正常发光．保持滑动变阻器滑片P的位置不变，闭合开关S1、S2，电流表示数又变化了1.5A．当开关S1、S2都闭合时，调节滑动变阻器滑片P的位置（滑片P不接触a端），电路消耗的总功率的最小值为20
20
W．分析：本题有4个过程，画出每一个过程的电路图．
（1）当开关S1、S2都断开时，滑动变阻器在b端时，灯泡L和滑动变阻器的整个电阻Rab串联在电路中，电路电流为I甲，如图甲．
（2）当开关S1、S2都断开时，滑动变阻器R的滑片P从b端滑到某一位置c时，如图乙．
滑动变阻器Rab接入电路的电阻减小6Ω，电源电压不变，总电阻减小，电流增大，I乙=I甲+0.1A，此时灯泡正常工作，根据灯泡的额定电压和额定功率，求出乙图中的电流．可以求出甲图中的电流．
根据甲乙两个过程的电源电压相等列出等式，求出滑动变阻器的最大阻值Rab、Rac、电源电压U．
（3）保持滑动变阻器滑片P的位置不变，闭合开关S1、S2，灯泡被短路，R0与Rac并联，如图丙，总电阻减小，干路电流增大，干路电流为I丙=I乙+1.5A．由总电压和总电流求出总电阻，求出R0的电阻．
（4）闭合开关S1、S2，R0与滑动变阻器并联，要使电路功率最小，电源电压一定，电路总电流最小，总电阻最大，R0是定值电阻，滑动变阻器连入电路的阻值最大时，电路总电阻最大，如图丁，求各支路电流，求总电流，求出消耗的最小功率．
（1）当开关S1、S2都断开时，滑动变阻器在b端时，灯泡L和滑动变阻器的整个电阻Rab串联在电路中，电路电流为I甲，如图甲．
（2）当开关S1、S2都断开时，滑动变阻器R的滑片P从b端滑到某一位置c时，如图乙．
滑动变阻器Rab接入电路的电阻减小6Ω，电源电压不变，总电阻减小，电流增大，I乙=I甲+0.1A，此时灯泡正常工作，根据灯泡的额定电压和额定功率，求出乙图中的电流．可以求出甲图中的电流．
根据甲乙两个过程的电源电压相等列出等式，求出滑动变阻器的最大阻值Rab、Rac、电源电压U．
（3）保持滑动变阻器滑片P的位置不变，闭合开关S1、S2，灯泡被短路，R0与Rac并联，如图丙，总电阻减小，干路电流增大，干路电流为I丙=I乙+1.5A．由总电压和总电流求出总电阻，求出R0的电阻．
（4）闭合开关S1、S2，R0与滑动变阻器并联，要使电路功率最小，电源电压一定，电路总电流最小，总电阻最大，R0是定值电阻，滑动变阻器连入电路的阻值最大时，电路总电阻最大，如图丁，求各支路电流，求总电流，求出消耗的最小功率．
解答：解：甲图：当开关S1、S2都断开时，灯泡L和滑动变阻器的整个电阻Rab串联在电路中，电路电流为I甲．
乙图：当开关S1、S2都断开时，滑片滑到c处，灯泡L和滑动变阻器的Rac串联，电路电阻减小，电流增大，I乙=I甲+0.1A，
此时灯泡正常工作，I乙=
=
=0.5A，
I甲=I乙-0.1A=0.5A-0.1A=0.4A，
灯泡电阻为：RL=
=
=12Ω，
根据甲乙两个过程电源电压相等，所以，I甲R甲=I乙R乙，
I甲（RL+Rab）=I乙（RL+Rac），
I甲（RL+Rab）=I乙（RL+Rab-6Ω），
0.4A×（12Ω+Rab）=0.5A×（12Ω+Rab-6Ω），
所以，Rab=18Ω，Rac=12Ω，
U=I甲（RL+Rab）=0.4A×（12Ω+18Ω）=12V．
丙图：保持滑动变阻器滑片P的位置不变，闭合开关S1、S2，灯泡被短路，R0与Rac并联，总电阻减小，电源电压不变，总电流增大，
I丙=I乙+1.5A=0.5A+1.5A=2A，
所以，电路总电阻为：R丙=
=
=6Ω，
R丙=
，
6Ω=
，
所以，R0=12Ω．
丁图：当开关S1、S2都闭合时，R0与滑动变阻器并联，要使总功率最小，电源电压一定，电路总电流最小，总电阻最大，滑动变阻器电阻最大，电路总电阻最大，所以，R0与Rab并联，
I0=
=
=1A，
Iab=
=
=
A，
所以，I丁=I0+Iab=1A+
A=
A，
P丁=UI丁=12V×
A=20W．
故答案为：20．
乙图：当开关S1、S2都断开时，滑片滑到c处，灯泡L和滑动变阻器的Rac串联，电路电阻减小，电流增大，I乙=I甲+0.1A，
此时灯泡正常工作，I乙=
| PL |
| UL |
| 3W |
| 6V |
I甲=I乙-0.1A=0.5A-0.1A=0.4A，
灯泡电阻为：RL=
| ||
| PL |
| (6V)2 |
| 3W |
根据甲乙两个过程电源电压相等，所以，I甲R甲=I乙R乙，
I甲（RL+Rab）=I乙（RL+Rac），
I甲（RL+Rab）=I乙（RL+Rab-6Ω），
0.4A×（12Ω+Rab）=0.5A×（12Ω+Rab-6Ω），
所以，Rab=18Ω，Rac=12Ω，
U=I甲（RL+Rab）=0.4A×（12Ω+18Ω）=12V．
丙图：保持滑动变阻器滑片P的位置不变，闭合开关S1、S2，灯泡被短路，R0与Rac并联，总电阻减小，电源电压不变，总电流增大，
I丙=I乙+1.5A=0.5A+1.5A=2A，
所以，电路总电阻为：R丙=
| U |
| I丙 |
| 12V |
| 2A |
R丙=
| R0Rac |
| R0+Rac |
6Ω=
| R0× 12Ω |
| R0+ 12Ω |
所以，R0=12Ω．
丁图：当开关S1、S2都闭合时，R0与滑动变阻器并联，要使总功率最小，电源电压一定，电路总电流最小，总电阻最大，滑动变阻器电阻最大，电路总电阻最大，所以，R0与Rab并联，
I0=
| U |
| R0 |
| 12V |
| 12Ω |
Iab=
| U |
| Rab |
| 12V |
| 18Ω |
| 2 |
| 3 |
所以，I丁=I0+Iab=1A+
| 2 |
| 3 |
| 5 |
| 3 |
P丁=UI丁=12V×
| 5 |
| 3 |
故答案为：20．
点评：本题属于比较难的电学计算题，本题通过开关的闭合与断开，滑动变阻器的滑片变化来完成电路的不同过程，针对此类习题，需要弄清几个过程，有几个过程，画几个电路图，找各个过程的不变量，把几个过程联系起来．不同过程电源电压相等是常见的一种方法，此方法即简单，又常用，又典型．
练习册系列答案
相关题目
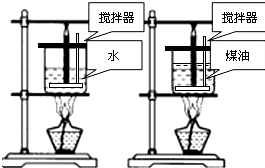（2009?怀柔区一模）为了比较水和沙子吸热本领的大小，小明做了如图所示的实验：在两个相同的烧杯中分别装有质量、初温都相同的水和沙子，用两个相同的酒精灯分别对其加热，得到表中的实验数据：
（2009?怀柔区一模）如图所示，某工地用固定在水平工作台上的卷扬机（其内部有电动机提供动力）通过滑轮组匀速提升货物，已知卷扬机的总质量为120kg，工作时拉动绳子的功率恒为400W．第一次提升质量为320kg的货物时，卷扬机对绳子的拉力为F1，对工作台的压力为N1；第二次提升质量为240kg的货物时，卷扬机对绳子的拉力为F2，对工作台的压力为N2．已知N2与N1之比为25﹕23，取g=10N/kg，绳重及滑轮的摩擦均可忽略不计．求：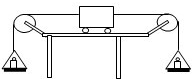
（2009?怀柔区一模）探究“二力平衡条件”的活动中，主要是通过探究力对物体的作用效果来实现探究目的．