题目内容
 如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:
如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:
(1)钩码重多少牛顿?
(2)圆球的密度是多少kg/m3?
(3)假如大气压强逐渐减小到零的过程中,杠杆还能平衡吗?若不平衡,怎样倾斜,请分析说明.
解:(1)玻璃管A处于平衡状态,所以受到平衡力的作用,即向下的大气压力、玻璃管的重力与杠杆对A向上的拉力、大气压通过管内水柱对其向上的压力相互平衡;
由此可得:P0S+G玻-(P0S-ρ水gLS)=FA,即:105Pa×2×10-3m2-2N-(105Pa×2×10-3m2-103kg/m3×10N/kg×0.4m×2×10-3m2)=FA.
求得:FA=10N,
又因为杠杆处于平衡状态,所以FA?OA=FB?OB,又OA=OB
所以FB=FA=10N,
根据动滑轮的省力公式:FB= (G动+G钩)
(G动+G钩)
变形得:G钩=2FB-G动=2×10N-1N=19N.
(2)由圆球处于平衡状态得:G球=F浮+F绳
由于是同一根绳子,所以F绳=FB=10N,
即:ρ球gV球=ρ水g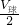 +FB;
+FB;
代入数据:ρ球×10N/kg×10-3m3=103kg/m3×10N/kg×0.5×10-3m3+10N,
求得:ρ球=1.5×103kg/m3.
(3)玻璃管处于平衡状态时:P0S+G玻-(P0S-ρ水gLS)=FA,
化简得:G玻+ρ水gLS=FA,
其中的ρ水gLS是由于大气压造成的,因此:
当①当P0≥ρ水gL时,FA=G玻+ρ水gLS=10N,杠杆仍平衡.
当②当P0<ρ水gL时,FA=G玻+P0S<10N,杠杆失去平衡,B端下降.
答:(1)钩码重19N;(2)圆球的密度是1.5×103kg/m3.(3)不再平衡,将向B端倾斜.
分析:(1)钩码的重力可以利用作用在杠杆B端的拉力结合动滑轮的重力,利用动滑轮的省力公式:FB= (G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.
(G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.
因此首先要知道作用在杠杆A端的力,这个力是由玻璃管提供的,从玻璃管现在所处的状态入手,求出作用在A端的力,从而可以解决此题.
(2)告诉了圆球的体积,要求圆球的密度,因此首先要求得圆球的重力.从圆球对动滑轮的拉力来求得圆球的重力.
(3)大气压的变化,决定了玻璃管受到的力的变化,只要玻璃管还处于平衡状态,杠杆就保持平衡,因此从玻璃管受力的情况的平衡方程,结合大气压的变化入手分析即可解决此题.
点评:此题涉及了:浮力的计算、杠杆的平衡条件、动滑轮的省力情况、大气压强、压力的计算等多个知识点.过程复杂,要求学生要有较强的逻辑思维能力.
解决此题时,可以从未知量入手分析,直到已知量为止.
能够根据物体处于平衡状态,得到力的方程是解决此题的关键.
由此可得:P0S+G玻-(P0S-ρ水gLS)=FA,即:105Pa×2×10-3m2-2N-(105Pa×2×10-3m2-103kg/m3×10N/kg×0.4m×2×10-3m2)=FA.
求得:FA=10N,
又因为杠杆处于平衡状态,所以FA?OA=FB?OB,又OA=OB
所以FB=FA=10N,
根据动滑轮的省力公式:FB=
 (G动+G钩)
(G动+G钩)变形得:G钩=2FB-G动=2×10N-1N=19N.
(2)由圆球处于平衡状态得:G球=F浮+F绳
由于是同一根绳子,所以F绳=FB=10N,
即:ρ球gV球=ρ水g
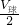 +FB;
+FB;代入数据:ρ球×10N/kg×10-3m3=103kg/m3×10N/kg×0.5×10-3m3+10N,
求得:ρ球=1.5×103kg/m3.
(3)玻璃管处于平衡状态时:P0S+G玻-(P0S-ρ水gLS)=FA,
化简得:G玻+ρ水gLS=FA,
其中的ρ水gLS是由于大气压造成的,因此:
当①当P0≥ρ水gL时,FA=G玻+ρ水gLS=10N,杠杆仍平衡.
当②当P0<ρ水gL时,FA=G玻+P0S<10N,杠杆失去平衡,B端下降.
答:(1)钩码重19N;(2)圆球的密度是1.5×103kg/m3.(3)不再平衡,将向B端倾斜.
分析:(1)钩码的重力可以利用作用在杠杆B端的拉力结合动滑轮的重力,利用动滑轮的省力公式:FB=
 (G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.
(G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.因此首先要知道作用在杠杆A端的力,这个力是由玻璃管提供的,从玻璃管现在所处的状态入手,求出作用在A端的力,从而可以解决此题.
(2)告诉了圆球的体积,要求圆球的密度,因此首先要求得圆球的重力.从圆球对动滑轮的拉力来求得圆球的重力.
(3)大气压的变化,决定了玻璃管受到的力的变化,只要玻璃管还处于平衡状态,杠杆就保持平衡,因此从玻璃管受力的情况的平衡方程,结合大气压的变化入手分析即可解决此题.
点评:此题涉及了:浮力的计算、杠杆的平衡条件、动滑轮的省力情况、大气压强、压力的计算等多个知识点.过程复杂,要求学生要有较强的逻辑思维能力.
解决此题时,可以从未知量入手分析,直到已知量为止.
能够根据物体处于平衡状态,得到力的方程是解决此题的关键.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:
如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求: 如图所示,一根均匀的木条AB长为L.将其放在水平桌面上,使B端伸出桌面
如图所示,一根均匀的木条AB长为L.将其放在水平桌面上,使B端伸出桌面 L,在伸出桌面部分的上方放一个长
L,在伸出桌面部分的上方放一个长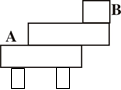
 L,在伸出桌面部分的上方放一个长
L,在伸出桌面部分的上方放一个长