题目内容
【题目】演绎式探究﹣探究太阳的引力系数:
(1)宇宙中任何两个物体之间都存在万有引力,万有引力的大小F引=G ![]() ,其中m1、m2分别为两个物体间的距离,万有引力常数G=6.67×10﹣11Nm2/kg2 . 物体间引力和距离一定时,两个物体质量m1、m2分的关系可以用如图中图线来表示.
,其中m1、m2分别为两个物体间的距离,万有引力常数G=6.67×10﹣11Nm2/kg2 . 物体间引力和距离一定时,两个物体质量m1、m2分的关系可以用如图中图线来表示. 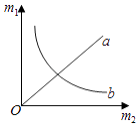
(2)行星绕恒星的运动可以近似地看作匀速圆周运动.行星受到一个恒定的指向恒星的向心力,向心力的大小F向=mω2r,其中m为行星质量,r为两星之间的距离,ω为行星做圆周运动的角速度,其大小等于单位时间内行星与恒星连线转过的角度.行星绕恒星运动一周所用的时间用周期T表示,角速度ω与转动周期T的关系为:ω= ![]() .行星所受向心力F向的大小等于恒星对行星的引力F引的大小. 每个星球对在它表面附件的物体都存在引力,引力与物体质量的比值叫作引力系数,用g表示,我们学过地球的引力系数g地=10N/kg.对于每个星球来讲,下列公式成立:R2g=GM,其中R为星球半径,g为星球引力系数,M为星球质量,万有引力常数G=6.67×10﹣11Nm2/kg2 .
.行星所受向心力F向的大小等于恒星对行星的引力F引的大小. 每个星球对在它表面附件的物体都存在引力,引力与物体质量的比值叫作引力系数,用g表示,我们学过地球的引力系数g地=10N/kg.对于每个星球来讲,下列公式成立:R2g=GM,其中R为星球半径,g为星球引力系数,M为星球质量,万有引力常数G=6.67×10﹣11Nm2/kg2 .
已知地球质量为m,地球到太阳的距离为L,太阳半径为R,地球的公转周期为T.请你推导出太阳的引力系数g日= ![]() .
.
【答案】
(1)b
(2)解:地球为太阳的行星,根据万有引力公式,F引=G ![]() =G
=G ![]() ﹣﹣﹣﹣﹣①,
﹣﹣﹣﹣﹣①,
它们之间的向心力:
F向=mω2r=m ![]() ﹣﹣﹣﹣﹣②;
﹣﹣﹣﹣﹣②;
因地球所受向心力F向的大小等于太阳对地球的引力F引的大小.由①②得:
F引=G ![]() =G
=G ![]() =m
=m ![]() L,
L,
即GM= ![]() ﹣﹣﹣﹣﹣﹣③;
﹣﹣﹣﹣﹣﹣③;
又对于每个星球来讲,R2g日=GM,
g日= ![]() ﹣﹣﹣﹣﹣④,将③代入④得:
﹣﹣﹣﹣﹣④,将③代入④得:
太阳的引力系数g日= 
【解析】解:(1)万有引力的大小F引=G ![]() ,其中m1、m2分别为两个物体间的距离,万有引力常数: G=6.67×10﹣11Nm2/kg2 . 由上式可知:
,其中m1、m2分别为两个物体间的距离,万有引力常数: G=6.67×10﹣11Nm2/kg2 . 由上式可知:
物体间引力和距离一定时,两个物体质量m1、m2分之积为定值,为反比例函数的关系,故可以用如图中图线b来表示.
所以答案是:(1)b;(2)如上所示.

 阅读快车系列答案
阅读快车系列答案【题目】回顾实验和探究(请将下列实验报告中的空缺部分填写完整):
(1)探究影响音调高低的因素:
过程 | 把钢尺紧按在桌面上,一端伸出桌边.拨动钢尺,保持振幅相同,运用的科学方法是法. |
|
现象 | 缩短钢尺伸出桌边的长度,发现钢尺振动得越来越 , 音调越来越 . | |
问题 | 在桌面上撒些碎纸片,敲击桌子,发现桌子发声的同时,碎纸片被弹起,由此证明声音是由物体产生的. | |
(2)探究凸透镜成像的规律:
现象 | 凸透镜的焦距是10cm.把蜡烛移至图中a点,光屏上出现了烛焰清晰的像,据此可制成 . 把蜡烛逐渐移近透镜,光屏上的像越来越(填“大”或“小”),但像始终是(填“正立”或“倒立”)的. |
|
方法 | 研究光现象时,将一束光看成一条光线,运用的科学方法是法. | |
问理 | 若蜡烛的像出现在了光屏的上半部,可能是由于烛焰、凸透镜和光屏的中心未调至 . | |








