��Ŀ����
����Ŀ��ͼ��Ϊ�о�����ֱ���˶���ʵ��װ�ã�һ���뾶Ϊ2cm�������ڴ�����������ֹ��ʢˮ�IJ����ܵף�ˮ��1m���Ƴ����������ڲ�������������ͼ��Ϊ����¶��ˮ��ǰ�˶��ٶ���ʱ��Ĺ�ϵͼ������v0=0.05m/s��ˮ���ܶ�Ϊ1.0��103kg/m3 �� ��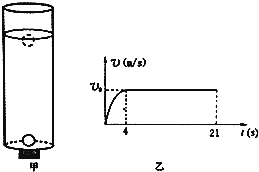
��1���Ƴ�����ǰ�������ܵ��ܵ�ˮ��ѹǿ��
��2�����ڲ���������������ǰ4s��ƽ���ٶȣ�
��3����֪������ʱ�ܵ�ˮ�����������ٶȵĹ�ϵΪf=kv����������V��ˮ���ܶ��æ�0��ʾ�����Ƶ�����ܶȱ���ʽ������ĸ��ʾ��
���𰸡�
��1��
�⣺�Ƴ�����ǰ�������ܵ��ܵ�ˮ��ѹǿ��
p=��gh=1.0��103kg/m3��10N/kg��1m=1��104Pa��
���Ƴ�����ǰ�������ܵ��ܵ�ˮ��ѹǿΪ1��104Pa
��2��
�⣺��ͼ��֪������¶��ˮ��ǰ�˶���ʱ��Ϊ21s��
����v= ![]() �ɵã�4��21s�������ľ��룺s0=v0t=0.05m/s��17s=0.85m��
�ɵã�4��21s�������ľ��룺s0=v0t=0.05m/s��17s=0.85m��
�����ڲ���������������ǰ4s�����ľ��룺s��=s��s0=1m��0.85m��2��0.02m=0.11m��
���ԣ����ڲ���������������ǰ4s��ƽ���ٶȣ�v��= ![]() =
= ![]() =0.0275m/s��
=0.0275m/s��
�����ڲ���������������ǰ4s��ƽ���ٶ�Ϊ0.0275m/s
��3��
�⣺��ͼ��֪����4��21sʱ��������������ƽ�⣬�����У�G+f=F����
����G=mg����= ![]() �ɵ�G=��Vg��
�ɵ�G=��Vg��
��֪��f=kv��F��=��0gV��
���Vg+kv=��0gV��
����ܶȦ�= ![]() =��0��
=��0�� ![]() ��
��
������ܶȱ���ʽΪ��=��0�� ![]()
����������1����֪ˮ����Ⱥ��ܶȣ�����p=��gh�����Ƴ�����ǰ�������ܵ��ܵ�ˮ��ѹǿ����2�������ٶȹ�ʽ���4��21s�������ľ��룬���ֱ����ˮ����ȼ�ȥ4��21s�������ľ��룬�ټ�ȥ���ֱ������Ϊ���ڲ���������������ǰ4s�����ľ��룬������v= ![]() �������ڲ���������������ǰ4s��ƽ���ٶȣ���3��������4��21sʱ���˶�״̬����������ƽ��ó�����������ܵ�����������֮��Ĺ�ϵ��Ȼ�������������ܶȸ�����ʽ�����Ƶ����⿼��Һ��ѹǿ���ٶȺ��ܶȵļ��㣬�ѵ��ڣ�3�����ؼ����������ȷ����������������������ƽ��ó�����������ܵ�����������֮��Ĺ�ϵ��
�������ڲ���������������ǰ4s��ƽ���ٶȣ���3��������4��21sʱ���˶�״̬����������ƽ��ó�����������ܵ�����������֮��Ĺ�ϵ��Ȼ�������������ܶȸ�����ʽ�����Ƶ����⿼��Һ��ѹǿ���ٶȺ��ܶȵļ��㣬�ѵ��ڣ�3�����ؼ����������ȷ����������������������ƽ��ó�����������ܵ�����������֮��Ĺ�ϵ��
�����㾫���������ܶȵļ����Һ���ѹǿ�ļ����ǽ����ĸ�������Ҫ֪���ܶȹ�ʽ���� = m/v��Һ���ڲ�ѹǿ�Ĺ�ʽ��p=��gh ��ָ�ܶ�,��λkg/m3,g=9.8N/kg, hָ���,��λ:m,ѹǿ��λ(Pa) ע�⣺h ָҺ�����ȣ���ij�㵽Һ��ľ��룮