题目内容
(2008?海淀区一模)小军在参加学校组织的拓展训练时,在湖边捡到一块漂亮的小石块,他想测出小石块的密度.小军书包里有一个水杯、一把钢尺和一些细线,他利用钢尺、水杯和细线设计了一个测量小石块密度的实验方案,以下是他设计的实验步骤,请将其补充完整.
(1)用一根细线拴好小石块系在钢尺的一端A,用另一根细线系在钢尺的某一适当位置O,手提细线将钢尺悬挂,钢尺恰好在水平位置平衡,
(2)把小石块浸没在盛有湖水的水杯中,将钢尺的悬挂点向远离A端移动到另一适当位置O′,使钢尺再次在水平位置平衡,
(3)已知湖水的密度为ρ水,利用上述测量出的物理量和已知量计算小石块密度的表达式为ρ石=
ρ水
ρ水.
(1)用一根细线拴好小石块系在钢尺的一端A,用另一根细线系在钢尺的某一适当位置O,手提细线将钢尺悬挂,钢尺恰好在水平位置平衡,
读出OA的长度L1和O点到钢尺中心距离L2
读出OA的长度L1和O点到钢尺中心距离L2
;(2)把小石块浸没在盛有湖水的水杯中,将钢尺的悬挂点向远离A端移动到另一适当位置O′,使钢尺再次在水平位置平衡,
读出O′A的长度L1′和O′点到钢尺中心距离L2′
读出O′A的长度L1′和O′点到钢尺中心距离L2′
;(3)已知湖水的密度为ρ水,利用上述测量出的物理量和已知量计算小石块密度的表达式为ρ石=
| L1′L2 |
| L1′L2-L1L2′ |
| L1′L2 |
| L1′L2-L1L2′ |
分析:(1)杠杆的平衡条件是:动力×动力臂=阻力×阻力臂;
(2)小石块在空气中时,对钢尺A端的拉力与它的重力相等;小石块浸没在水中时,对钢尺A端的拉力等于石块重力与浮力的差.
(3)根据小军的两次操作,画出示意图,再结合浮力知识和杠杆的平衡条件,经过推导计算就可以得到石块密度的表达式.
(2)小石块在空气中时,对钢尺A端的拉力与它的重力相等;小石块浸没在水中时,对钢尺A端的拉力等于石块重力与浮力的差.
(3)根据小军的两次操作,画出示意图,再结合浮力知识和杠杆的平衡条件,经过推导计算就可以得到石块密度的表达式.
解答:解:(1)用一根细线拴好小石块系在钢尺的一端A,用另一根细线系在钢尺的某一适当位置O,手提细线将钢尺悬挂,钢尺恰好在水平位置平衡,读出OA的长度L1和O点到钢尺中心距离L2,如下图所示:

根据杠杆的平衡条件可得:G石×L1=G尺×L2…①;
(2)把小石块浸没在盛有湖水的水杯中,将钢尺的悬挂点向远离A端移动到另一适当位置O′,使钢尺再次在水平位置平衡,读出O′A的长度L1′和O′点到钢尺中心距离L2′,如下图所示:
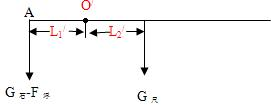
根据杠杆的平衡条件可得:(G石-F浮)×L1′=G尺×L2′…②;
(3)①式与②式相比得:
=
,因为G石=ρ石V石g,F浮=ρ水gV石,代入式子,进一步化简得:
ρ石=
ρ水.
故答案为:(1)读出OA的长度L1和O点到钢尺中心距离L2;
(2)读出O′A的长度L1′和O′点到钢尺中心距离L2′;
(3)
ρ水.

根据杠杆的平衡条件可得:G石×L1=G尺×L2…①;
(2)把小石块浸没在盛有湖水的水杯中,将钢尺的悬挂点向远离A端移动到另一适当位置O′,使钢尺再次在水平位置平衡,读出O′A的长度L1′和O′点到钢尺中心距离L2′,如下图所示:

根据杠杆的平衡条件可得:(G石-F浮)×L1′=G尺×L2′…②;
(3)①式与②式相比得:
| G石×L1 |
| (G石-F浮)×L1′ |
| L2 |
| L2′ |
ρ石=
| L1′L2 |
| L1′L2-L1L2′ |
故答案为:(1)读出OA的长度L1和O点到钢尺中心距离L2;
(2)读出O′A的长度L1′和O′点到钢尺中心距离L2′;
(3)
| L1′L2 |
| L1′L2-L1L2′ |
点评:本题重点考查学生对浮力知识和杠杆平衡条件的应用,关键是知道第二次石块浸没在水中时,拉动钢尺的力为石块重力和浮力之差.

练习册系列答案
相关题目
 (2008?海淀区一模)小玲同学在探究“导体的电阻跟哪些因素有关”的问题时,选择了如下图所示的器材.演示板上固定了四根金属丝,a,b,c三条长度均为1m,d的长度为0.5m,a、b的横截面积相同,材料不同;a、c的材料相同,但c的横截面积大于a;a、d的材料和横截面积都相同.该同学记录数据如下表.
(2008?海淀区一模)小玲同学在探究“导体的电阻跟哪些因素有关”的问题时,选择了如下图所示的器材.演示板上固定了四根金属丝,a,b,c三条长度均为1m,d的长度为0.5m,a、b的横截面积相同,材料不同;a、c的材料相同,但c的横截面积大于a;a、d的材料和横截面积都相同.该同学记录数据如下表. (2008?海淀区一模)如图所示,电路中电源两端电压保持不变,滑动变阻器的最大阻值为R3.将滑动变阻器的滑片P置于A端,只闭合开关S1时,电压表V1的示数为U1,电压表V2的示数为U2;将滑动变阻器的滑片P置于B端,仍只闭合开关S1时,电压表V1的示数为U1′,电压表V2的示数为U2′,R1消耗的电功率为0.72W.已知U1:U1′=4:7,U2:U2′=2:1,R2=12Ω.
(2008?海淀区一模)如图所示,电路中电源两端电压保持不变,滑动变阻器的最大阻值为R3.将滑动变阻器的滑片P置于A端,只闭合开关S1时,电压表V1的示数为U1,电压表V2的示数为U2;将滑动变阻器的滑片P置于B端,仍只闭合开关S1时,电压表V1的示数为U1′,电压表V2的示数为U2′,R1消耗的电功率为0.72W.已知U1:U1′=4:7,U2:U2′=2:1,R2=12Ω. (2008?海淀区一模)图25是液压汽车起重机从水中打捞重物的示意图.A是动滑轮,B是定滑轮,C是卷扬机,D是油缸,E是柱塞.作用在动滑轮上共三股钢丝绳,卷扬机转动使钢丝绳带动动滑轮上升提取重物,被打捞的重物体积V=0.5m3.若在本次打捞前起重机对地面的压强p0=2.0×107Pa,当物体在水中匀速上升时起重机对地面的压强p1=2.375×107Pa,物体完全出水后起重机对地面的压强p2=2.5×107Pa.假设起重时柱塞沿竖直方向,物体出水前、后柱塞对吊臂的支撑力分别为N1和N2,N1与N2之比为19:24.重物出水后上升的速度v=0.45m/s.吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计.(g取10N/kg)求:
(2008?海淀区一模)图25是液压汽车起重机从水中打捞重物的示意图.A是动滑轮,B是定滑轮,C是卷扬机,D是油缸,E是柱塞.作用在动滑轮上共三股钢丝绳,卷扬机转动使钢丝绳带动动滑轮上升提取重物,被打捞的重物体积V=0.5m3.若在本次打捞前起重机对地面的压强p0=2.0×107Pa,当物体在水中匀速上升时起重机对地面的压强p1=2.375×107Pa,物体完全出水后起重机对地面的压强p2=2.5×107Pa.假设起重时柱塞沿竖直方向,物体出水前、后柱塞对吊臂的支撑力分别为N1和N2,N1与N2之比为19:24.重物出水后上升的速度v=0.45m/s.吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计.(g取10N/kg)求: