Question

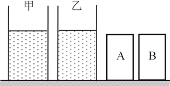
【题目】两个薄壁圆柱形容器甲、乙放置在水平地面上，容器底面积均为0.01米2、容器重力均为G0，容器内盛有相同高度的水，如图所示。将两个密度不同、体积均为1×10-3米3的实心光滑柱体A、B分别竖直放入甲、乙两容器中，水对容器底部的压强p水和容器对地面的压强p容如下表所示。

压强	放入A柱体	放入B柱体
p水（帕）	1470	1960
p容（帕）	1960	2940

（1）求放入A柱体后，甲容器对水平地面的压力。

（2）通过计算确定容器的重力。

（3）判断柱体B在水中的浮沉状态，并说明你的判断依据。

Answer 1

【答案】（1）19.6牛（2）4.9牛（3）沉底

【解析】

(1)放入A柱体后，甲容器对水平地面的压力

F=p容S=1960Pa×0.01m2=19.6N；

(2)因为

p水B＞p水A

由p=ρgh可得，

h水B＞h水A

由V=Sh可得

V排 B＞V排 A

A一定漂浮，且无水溢出。因为

G0+G水+GA＝p容AS

在柱形容器中

G水+F浮A＝G水+GA＝p水AS

G0＝(p容A- p水A)S＝(1960Pa-1470Pa) ×0.01m2=4.9N；

(3)同理

G0+G水+GB-G溢＝p容BS ①

G水+F浮B-G溢＝p水BS ②

由① ②得

GB-F浮B＝(p容B- p水B)S-G0＝(2940Pa-1960Pa)×0.01m2-4.9N＝4.9N＞0，

B一定是沉底的。

答：(1)放入A柱体后，甲容器对水平地面的压力是19.6N；

(2)通过计算确定容器的重力是4.9N；

(3)沉底，见解析。