题目内容
【题目】从地面上搬起重物常见的做法是弯腰(如图甲)或下蹲弯曲膝盖(如图乙).对此可建立一个模型:把脊柱简化为杠杆,如图丙所示.脊柱可绕骶骨(轴)O 转动,腰背部复杂肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,在B点挂一重物代替箱子.用测力计沿F1方向拉,使模型保持与水平面成某一角度静止,可测出腰背部复杂肌肉拉力的大小.已知OA长45cm,AB长15cm(g=10N/kg). 
(1)当脊柱与水平面夹角α=60°,搬起一个5kg重的箱子,求搬箱子的力F2的力臂大小.
(2)如图甲的搬运方式,脊柱与水平面的夹角α=0°,若搬运同样重的箱子,请判断脊柱肌肉所用的力F1的大小与α的关系,并证明.
(3)由证明可知平时搬运货物选择哪种方法更好?(填:甲或乙).
【答案】
(1)解:由图丙画出动力臂和阻力臂如图所示:
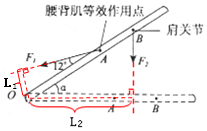 ,
,
由题知,OA长45cm,AB长15cm,所以OB=OA+AB=45cm+15cm=60cm,
当脊柱与水平面夹角α=60°,所以∠ABF2=30°,
所以F2的力臂:L2=OB×cosα=OB×cos60°=60cm× ![]() =30cm
=30cm
答:当脊柱与水平面夹角α=60°,搬箱子的力F2的力臂为30cm.
(2)解:由题知,F1方向与脊柱夹角为12°且保持不变,
所以动力臂:L1=sin12°×OA=sin12°×45cm,
阻力臂:L2=cosα×OB=cosα×60cm,
F2=mg=5kg×10N/kg=50N,
由杠杆的平衡条件F1L1=F2L2可得:F1×sin12°×45cm=50N×cosα×60cm,
所以:F1= ![]() N
N
答:脊柱肌肉所用的力F1的大小与α的关系为F1= ![]() N
N
(3)乙
【解析】(3)比较甲、乙两种姿势结合图丙可知,甲姿势开始时角α为0°,乙姿势开始时角α大于0°, 因为sin12°为定值,且α在0﹣90°之间变化时,随α增大,cosα逐渐减小,由F1= ![]() N可得,乙姿势更省力一些,故用乙方法好.
N可得,乙姿势更省力一些,故用乙方法好.
(1)力臂从支点到力的作用线的距离,由此画出F2的力臂再计算;(2)由杠杆示意图表示出动力臂和阻力臂,根据杠杆的平衡条件得出F1的大小与α的关系;(3)由两种搬运货物方式,结合F1的大小与α的关系式分析F1大小情况,从而得到结论.
【考点精析】通过灵活运用杠杆中最小力的问题,掌握判断是省力杠杆还是费力杠杆,先确定动力臂和阻力臂,再比较动力臂和阻力臂的大小.动力臂大,动力就小.为省力杠杆.反之,为费力杠杆即可以解答此题.