题目内容
 如图所示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的
如图所示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的| 1 | 5 |
分析:(1)甲乙分别挂在杠杆的两端,杠杆平衡,根据杠杆平衡条件列出等式G甲×OA=G乙×OB,
(2)甲浸没在水中,杠杆处于平衡状态,根据杠杆平衡条件列出等式,求出甲乙的体积的关系,也就是质量的关系.
(2)甲浸没在水中,杠杆处于平衡状态,根据杠杆平衡条件列出等式,求出甲乙的体积的关系,也就是质量的关系.
解答:解:(1)如图杠杆平衡,根据杠杆平衡条件得,G甲×OA=G乙×OB,整理可得:OB=
=
=
;
(2)甲浸没在水中,杠杆平衡,支点必须向右越大,增大甲的力臂,根据杠杆平衡条件得,
(G甲-F浮)×O′A=G乙×O′B,
(G甲-ρ水gV甲)×(OA+
OA)=G乙×(OB-
OA);
(ρV甲g-ρ水gV甲)×
OA=ρV乙g×(
-
OA)=ρV乙g×(
-
OA);
整理可得:
=
=
=
因为甲乙密度相等,所以质量之比就等于体积之比,
所以甲、乙两个物体的质量之比为2:1.
答:甲、乙两个物体的质量之比为2:1.
| G甲×OA |
| G乙 |
| ρV甲g×OA |
| ρV乙g |
| V甲×OA |
| V乙 |
(2)甲浸没在水中,杠杆平衡,支点必须向右越大,增大甲的力臂,根据杠杆平衡条件得,
(G甲-F浮)×O′A=G乙×O′B,
(G甲-ρ水gV甲)×(OA+
| 1 |
| 5 |
| 1 |
| 5 |
(ρV甲g-ρ水gV甲)×
| 6 |
| 5 |
| G甲×OA |
| G乙 |
| 1 |
| 5 |
| V甲×OA |
| V乙 |
| 1 |
| 5 |
整理可得:
| V甲 |
| V乙 |
| ρ |
| 6ρ水-ρ |
| 4.0×103kg/m3 |
| 6×1.0×103kg/m3-4.0×103kg/m3 |
| 2 |
| 1 |
因为甲乙密度相等,所以质量之比就等于体积之比,
所以甲、乙两个物体的质量之比为2:1.
答:甲、乙两个物体的质量之比为2:1.
点评:本题两次利用杠杆平衡条件列出两个等式,联立方程求解即可,对于杠杆平衡问题,一般要根据杠杆平衡条件列等式求解.

练习册系列答案
相关题目
 (2010?房山区二模)如图所示,用带有水桶的滑轮组把水从蓄水池中提到h=7m高的阳台,空水桶B的质量为2kg,POQ为固定支架,轻质杠杆MN可绕固定支点O转动,OM:ON=5:1,A为正方体配重,底面积为10-2m2,用绳索与杠杆N端相连,并保持杠杆水平.小明用力F1可匀速提升一满桶水,用力F2可匀速提升半桶水,且F1-F2=150N,F1:F2=32:17,(不计定滑轮的质量、绳子的质量及轮与轴的摩擦,g=10N/kg)求:
(2010?房山区二模)如图所示,用带有水桶的滑轮组把水从蓄水池中提到h=7m高的阳台,空水桶B的质量为2kg,POQ为固定支架,轻质杠杆MN可绕固定支点O转动,OM:ON=5:1,A为正方体配重,底面积为10-2m2,用绳索与杠杆N端相连,并保持杠杆水平.小明用力F1可匀速提升一满桶水,用力F2可匀速提升半桶水,且F1-F2=150N,F1:F2=32:17,(不计定滑轮的质量、绳子的质量及轮与轴的摩擦,g=10N/kg)求:
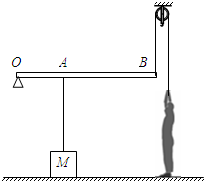 (2008?昌平区一模)如图所示,一正方体合金块M的边长为20cm,把它挂在以O为支点的轻质杠杆的A点处,一个重为640N的人在杠杆的B点通过定滑轮用力F1使杠杆在水平位置平衡,此时M对水平地面的压强为1.1×104Pa,人对水平地面的压强为1.45×104Pa;若把M浸没于水中(M与容器底不接触),人用力F2仍使杠杆在水平位置平衡,此时人对地面的压强为1.15×104 Pa;已知人单独站在水平地面上,对地面的压强为1.6×104 Pa.(g取10N/kg)求:
(2008?昌平区一模)如图所示,一正方体合金块M的边长为20cm,把它挂在以O为支点的轻质杠杆的A点处,一个重为640N的人在杠杆的B点通过定滑轮用力F1使杠杆在水平位置平衡,此时M对水平地面的压强为1.1×104Pa,人对水平地面的压强为1.45×104Pa;若把M浸没于水中(M与容器底不接触),人用力F2仍使杠杆在水平位置平衡,此时人对地面的压强为1.15×104 Pa;已知人单独站在水平地面上,对地面的压强为1.6×104 Pa.(g取10N/kg)求: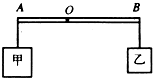 如图所示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的
如图所示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的 ,求:甲、乙两个物体的质量之比.
,求:甲、乙两个物体的质量之比.