题目内容
【题目】小雨观察到游乐场的过山车可以底朝上在圆形轨道上运动,游客却不会掉下来,他想探索其中的奥秘,做了以下两个探究:



(![]() )探究一:如图甲所示,小球由
)探究一:如图甲所示,小球由![]() 点沿光滑轨道自由运动到
点沿光滑轨道自由运动到![]() 点,小球到达
点,小球到达![]() 点的速度
点的速度![]() 与高度
与高度![]() 和小球质量
和小球质量![]() 的关系,数据如表一.
的关系,数据如表一.
表一
实验次数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
则小球到达B点的速度v与_________有关,且v2=k1______。
(![]() )探究二:如图乙所示,小球以一定速度从
)探究二:如图乙所示,小球以一定速度从![]() 点沿光滑的竖直圆形轨道运动,恰好通过最高点
点沿光滑的竖直圆形轨道运动,恰好通过最高点![]() ,小球在
,小球在![]() 点的速度
点的速度![]() 与轨道半径
与轨道半径![]() 的关系,数据如表二.
的关系,数据如表二.
由小球在![]() 点的速度
点的速度![]() 与轨道半径
与轨道半径![]() 的关系式为__________.
的关系式为__________.
表二:
实验次数 |
|
|
|
|
|
|
|
|
|
|
|
(![]() )如图丙所示,将甲、乙两轨道组合后,小球从
)如图丙所示,将甲、乙两轨道组合后,小球从![]() 点沿光滑轨道自由运动,若
点沿光滑轨道自由运动,若![]() ,要使小球经过
,要使小球经过![]() 点后能恰好通过
点后能恰好通过![]() 点,则
点,则![]() __________.
__________.
【答案】高度h h v2=50m/s2×r 1m
【解析】
(1)表格一:由1、2次实验数据可知,质量相同时,下滑的高度越高到达B点速度的平方越大,且小球下落高度的倍数和到达B点速度平方的倍数相等,即小球到达B点的速度v的平方与高度h成正比;由2、3次实验数据可知,小球下滑的高度相同时,质量不同的小球到达B点速度的平方相等,则小球到达B点的速度与小球的质量无关,综上可知,小球到达B点的速度v与高度h有关,且v2=k1h;
(2)表格二:由三次实验数据可知,轨道半径的变化数据和v2的变化倍数相等,则小球在B点的速度v2与轨道半径r成正比,设为v2=kr,把v2=7.5m2/s2、r=0.15m代入可得,k=50m/s2,小球在B点的速度v与轨道半径r的关系式为v2=50m/s2×r;
(3)由表格一数据可知,当v2=4.0m2/s2时h=0.2m,则k1=v2/h=(4.0m2/s2)/0.2m=20m/s2,小球从A点沿光滑轨道自由运动,恰好通过C点时,由v2=50m/s2×r可得,B点的速度平方:v2B=50m/s2×r=50m/s2×0.4m=20m2/s2,
由v2=k1h可得,小球下落的高度: hB=v2B/k1=(20m2/s2)/(20m/s2)=1m。

【题目】阅读短文,回答问题.
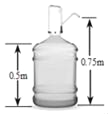
在我国随着人民生活水平的提高,汽车开始进入普通百姓家庭.小明同学家买了一辆崭新的汽车(如图),部分相关参数配置如下表所示.

参数 | |||||
车身质量 | 1200kg | 油箱容积 | 50L | 理论油耗 | 6L/100km |
全车长度 | 4269mm | 车身宽度 | 1686mm | 车身高度 | 1492mm |
(1)经过加油站时,小明闻到汽油味,这是由于_________.加油站规定工作人员在上班时间不能穿化纤布料做的衣服,这是因为化纤布料容易发生摩擦_________,存在火灾隐患.
(2)2017年3月,发改委对汽油价格进行了微小调整.和大多数物质一样,汽油也有热胀冷缩的性质,随着气温的上升,汽油密度会_________(“变大”或“变小”),受此因素影响,在每吨汽油价格不变的情况下,每升汽油的价格应_________(“上调”或“下调”).
(3)如果他家的汽车正常行驶100km(汽油的密度为0.7g/cm3).则查阅上表中的参数可知,理论情况下该车行驶100km所消耗的汽油的质量是_________kg.