题目内容
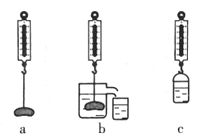
【题目】测量液体密度的仪器叫做密度计.图(a)和图(b)是自制的简易密度计,它是在木棒的一端缠绕一些铜丝做成的,将其放入盛有不同液体的两个烧杯中.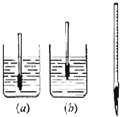
(1)请判断哪杯液体密度大,并说明理由.
(2)实验室的密度计的上部是一个用来标刻度的空心圆柱形玻璃管,管下部为一玻璃泡,内装有铅粒.某密度计圆柱形玻璃管长L=10cm,横截面积S=2.5cm2 , 该密度计总质量m=20g,将它放入水中静止时,水面距玻璃管上端为4cm;将此密度计放入未知液体中静止时,发现液面距玻璃管上端为2cm.求这种液体的密度以及密度计玻璃管上能标出的最大刻度值和最小刻度值.(已知水的密度为1.0×103kg/m3 , g=10N/kg)
【答案】
(1)
同一个密度计放在不同液体中都漂浮,则F浮a=F浮b=G,
由图知密度计排开液体的体积V排a>V排b,根据F浮=ρ液V排g可知:ρa<ρb.
(2)
解:密度计的质量m=20g=0.02kg,则G=mg=0.02kg×10N/kg=0.2N;
当置于水中时,F浮1=G=0.2N;,
由F浮=ρ水gV排可得:
V排水= ![]() =
= ![]() =2×10﹣5m2,
=2×10﹣5m2,
圆柱形玻璃管进入水的体积V1=S(h﹣h1)=2.5cm2×(10cm﹣4cm)=15cm3=1.5×10﹣5m3;
所以管下部玻璃泡的体积V0=V排水﹣V1=2×10﹣5m2﹣1.5×10﹣5m2=5×10﹣6m2,
放入未知液体中静止时,圆柱形玻璃管进入液体的体积V2=S(h﹣h2)=2.5cm2×(10cm﹣2cm)=20cm3=2×10﹣5m3;
则V排液=V0+V2=5×10﹣6m2+2×10﹣5m3=2.5×10﹣5m3;
由于密度计都是处于漂浮状态,则F浮2=G=0.2N;,
由F浮=ρ水gV排可得:
ρ液= ![]() =
= ![]() =0.8×103kg/m3.
=0.8×103kg/m3.
当密度计上部的圆柱形玻璃管全部露出液面时,所测液体密度值为最大,
因为F浮=G,所以,ρ最大gV0=G,
则ρ最大= ![]() =
= ![]() =4×103kg/m3.
=4×103kg/m3.
当密度计上部的圆柱形玻璃管全部浸没液面时,所测液体密度值为最小,
圆柱形玻璃管的体积V=Sh=2.5cm2×10cm=25cm3=2.5×10﹣5m3;
V排最大=V0+V=5×10﹣6m2+2.5×10﹣5m3=3×10﹣5m3;
因为F浮=G,所以,ρ最小g(V0+Sh)=G,
则ρ最小= ![]() =
= ![]() ≈0.67×103kg/m3.
≈0.67×103kg/m3.
答:这种液体的密度为0.8×103kg/m3;密度计玻璃管上能标出的最大刻度值和最小刻度值分别为4×103kg/m3、0.67×103kg/m3.
【解析】①从图可知,密度计放在甲、乙液体中都漂浮,受到的浮力都等于密度计受到的重力,从图可以得出密度计排开液体体积的大小关系,再根据阿基米德原理分析液体的密度大小关系.②求出密度计受到的重力,把密度计放在水里漂浮,利用物体的漂浮条件求受到水的浮力;再利用阿基米德原理求排开水的体积,根据玻璃管上端漏出的长度求出玻璃管浸入水的体积,继而可求出管下部玻璃泡的体积.
将此密度计放入未知液体中静止时,根据玻璃管上端漏出的长度和管下部玻璃泡的体积求出排开液体的体积,利用物体的漂浮条件和阿基米德原理即可求出液体密度;
当密度计上部的圆柱形玻璃管全部露出液面时,所测液体密度值为最大,再利用物体的漂浮条件和阿基米德原理求解.
当密度计上部的圆柱形玻璃管全部浸没液面时,所测液体密度值为最小,再利用物体的漂浮条件和阿基米德原理求解.
本题考查了学生对阿基米德原理和物体的漂浮条件的掌握和运用,利用好密度计测液体密度时漂浮(F浮=G)是本题的关键.
【考点精析】通过灵活运用物体的浮沉条件及其应用,掌握物体的浮沉条件:浸没在液体中的物体 F浮>G 时上浮,F浮 = G 时悬浮,F浮 <G 时下沉.物体浮沉条件的应用举例:(1)轮船(2)潜水艇(3)气球(4)飞艇、热气(5)密度计(密度计的刻度是从上到下刻度变大,刻度不均匀,且刻度无单位.)即可以解答此题.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案【题目】小莉根据下列表中的数据,得出下列四个结论,其中不正确的是( )
物质 | 密度ρ/(kg/m﹣3) | 物质 | 熔点/℃ | 物质 | 比热容 | |
煤油 | 0.8×103 | 铜 | 1083 | 干泥土 | 0.84×103 | |
纯水 | 1.0×103 | 铝 | 660 | 水 | 4.2×103 | |
铜 | 8.9×103 | 铅 | 328 | 铜 | 0.39×103 | |
铝 | 2.7×103 | 锡 | 232 | 铝 | 0.88×103 |
A.质量相等的纯水和煤油,纯水的体积较小
B.质量相等的铜块和铝块,放出相等热量,铝快温度降低得较多
C.用来熔化锡的器皿可以用铜制成
D.质量相等的干泥土和水,吸收相等热量,干泥土温度升高得较多