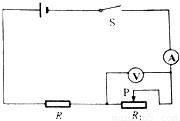
题目内容
如图所示电路中,定值电阻R1=40Ω,R2为滑动变阻器,要求通过R1的电流在0.05A~0.25A的范围内变化,问:(1)电路两端的电压U最小为多少?
(2)滑动变阻器R2的最大阻值至少应为多少?

【答案】分析:(1)要达到通过R1的电流变化范围,那么当干路电流为0.25A时,滑动变阻器R2的阻值最小;由于R1、R2串联,根据串联分压原理知:当R2分得电压最小(为0)时,电源电压最小,由此确定解题思路.
(2)当滑动变阻器阻值最大时,电路中的电流最小(I=0.05A),根据R= 求出滑动变阻器的阻值.
求出滑动变阻器的阻值.
解答:已知:R1=40Ω,I最小=0.05A,I最大=0.25A
求:U,R
解:(1)当滑动变阻器的阻值为0时,R1两端的电压为电路两端的最小电压,并且此时电路的电流值最大,所以电路两端的电压为:U=I最大R1=0.25A×40Ω=10V;
(2)当电路中的电流最小时,变阻器接入电路的阻值最大,即滑动变阻器R2的最大阻值至少为:
R= =
= =160Ω;
=160Ω;
答:电路两端的电压U最小为10V,滑动变阻器R2的最大阻值至少应为160Ω.
点评:会根据串联电路特点分析电路,会熟练应用欧姆定律进行计算.
(2)当滑动变阻器阻值最大时,电路中的电流最小(I=0.05A),根据R=
 求出滑动变阻器的阻值.
求出滑动变阻器的阻值.解答:已知:R1=40Ω,I最小=0.05A,I最大=0.25A
求:U,R
解:(1)当滑动变阻器的阻值为0时,R1两端的电压为电路两端的最小电压,并且此时电路的电流值最大,所以电路两端的电压为:U=I最大R1=0.25A×40Ω=10V;
(2)当电路中的电流最小时,变阻器接入电路的阻值最大,即滑动变阻器R2的最大阻值至少为:
R=
 =
= =160Ω;
=160Ω;答:电路两端的电压U最小为10V,滑动变阻器R2的最大阻值至少应为160Ω.
点评:会根据串联电路特点分析电路,会熟练应用欧姆定律进行计算.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
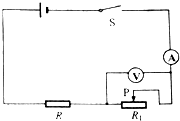 (2010?自贡)如图所示电路中,定值电阻R=5Ω,R1为滑动变阻器,电源电压保持不变.当滑片P在变阻器最左端时,电流表示数为1.2A;当滑片P在变阻器最右端时,电压表示数为4V.
(2010?自贡)如图所示电路中,定值电阻R=5Ω,R1为滑动变阻器,电源电压保持不变.当滑片P在变阻器最左端时,电流表示数为1.2A;当滑片P在变阻器最右端时,电压表示数为4V. 如图所示电路中,定值电阻R1=40Ω,R2为滑动变阻器,要求通过R1的电流在0.05A~0.25A的范围内变化,
如图所示电路中,定值电阻R1=40Ω,R2为滑动变阻器,要求通过R1的电流在0.05A~0.25A的范围内变化,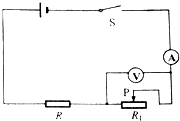 如图所示电路中,定值电阻R=5Ω,R1为滑动变阻器,电源电压保持不变.当滑片P在变阻器最左端时,电流表示数为1.2A;当滑片P在变阻器最右端时,电压表示数为4V.
如图所示电路中,定值电阻R=5Ω,R1为滑动变阻器,电源电压保持不变.当滑片P在变阻器最左端时,电流表示数为1.2A;当滑片P在变阻器最右端时,电压表示数为4V.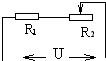 如图所示电路中,定值电阻R1=40Ω,R2为滑动变阻器,要求通过R1的电流在0.05A~0.25A的范围内变化,
如图所示电路中,定值电阻R1=40Ω,R2为滑动变阻器,要求通过R1的电流在0.05A~0.25A的范围内变化,