题目内容
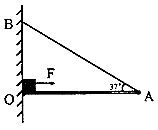
如图所示,有一块平直的轻质木板(木板重力不计),其左端连接在转动轴O处,其右端A 用一根细绳系在竖直墙上的B 处,此时木板恰好水平,∠BAO=30°,细绳能承受的最大拉力为10N,OA两点间距是100cm.现将一个重为20N的物块(边长忽略不计)放在木板上O点处,让它在一个大小为8N的水平拉力作用下以2cm/s的速度向右做匀速直线运动,当小物块运动到C点时,细绳被拉断.求:
(1)OC间的距离是多大?
(2)小物块在木板上运动了多长时间,细绳才被拉断?
(3)在细绳AB被拉断之前,拉力F对小物块做了多少功?做功功率为多大?

【答案】分析:(1)如图所示,当物块到达C点时,木板受到物块的压力、细绳的拉力,求出拉力和压力的力臂,根据杠杆的平衡条件求OC的大小;
(2)求出了OC的大小,知道物块的移动速度,利用速度公式求所用时间;
(3)知道拉力F大小和物块移动距离,利用W=Fs求拉力做功;又知道做功时间,利用功率公式求拉力做功功率.
解答:解:
(1)如图所示,当物块到达C点时,木板受到物块的压力F1=G=20N,F2=10N,
在Rt△AOD中,∠DAO=30°,OD= OA=
OA= ×100cm=50cm,
×100cm=50cm,
∵木板平衡,
∴F1×OC=F2×OD,
即:20N×OC=10N×50cm,
∴OC=25cm;
(2)t=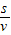 =
=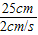 =12.5s;
=12.5s;
(3)拉力做功:
W=Fs=8N×0.25m=2J,
拉力做功功率:
P=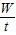 =
=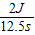 =0.16W.
=0.16W.
答:(1)OC间的距离是25cm;
(2)小物块在木板上运动了12.5s,细绳才被拉断;
(3)在细绳AB被拉断之前,拉力F对小物块做了2J的功,做功功率为0.16W.
点评:本题考查了学生对杠杆平衡条件、速度公式、功的公式、功率公式的掌握和运用,关键是利用杠杆平衡条件的利用.
(2)求出了OC的大小,知道物块的移动速度,利用速度公式求所用时间;
(3)知道拉力F大小和物块移动距离,利用W=Fs求拉力做功;又知道做功时间,利用功率公式求拉力做功功率.
解答:解:
(1)如图所示,当物块到达C点时,木板受到物块的压力F1=G=20N,F2=10N,

在Rt△AOD中,∠DAO=30°,OD=
 OA=
OA= ×100cm=50cm,
×100cm=50cm,∵木板平衡,
∴F1×OC=F2×OD,
即:20N×OC=10N×50cm,
∴OC=25cm;
(2)t=
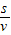 =
=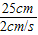 =12.5s;
=12.5s;(3)拉力做功:
W=Fs=8N×0.25m=2J,
拉力做功功率:
P=
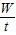 =
=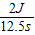 =0.16W.
=0.16W.答:(1)OC间的距离是25cm;
(2)小物块在木板上运动了12.5s,细绳才被拉断;
(3)在细绳AB被拉断之前,拉力F对小物块做了2J的功,做功功率为0.16W.
点评:本题考查了学生对杠杆平衡条件、速度公式、功的公式、功率公式的掌握和运用,关键是利用杠杆平衡条件的利用.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
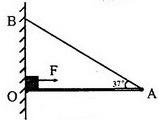 如图所示,有一块平直的轻质木板(木板重力不计),其左端连接在转动轴O处,其右端A用一根细绳系在竖直墙B处,此时木板恰好水平,夹角∠BAO=37°,细绳能承受的最大拉力为10N,OB两点间距是5m,现将一个重量为10N的小物块放在木板上O点附近(可视为在O点),让它在一个大小为5N的水平拉力作用下以2m/s的速度向右做匀速直线运动(已知sin37°=0.6,sin53°=0.8).
如图所示,有一块平直的轻质木板(木板重力不计),其左端连接在转动轴O处,其右端A用一根细绳系在竖直墙B处,此时木板恰好水平,夹角∠BAO=37°,细绳能承受的最大拉力为10N,OB两点间距是5m,现将一个重量为10N的小物块放在木板上O点附近(可视为在O点),让它在一个大小为5N的水平拉力作用下以2m/s的速度向右做匀速直线运动(已知sin37°=0.6,sin53°=0.8). 如图所示,有一块平直的轻质木板(木板重力不计),其左端连接在转动轴O处,其右端A 用一根细绳系在竖直墙上的B 处,此时木板恰好水平,∠BAO=30°,细绳能承受的最大拉力为10N,OA两点间距是100cm.现将一个重为20N的物块(边长忽略不计)放在木板上O点处,让它在一个大小为8N的水平拉力作用下以2cm/s的速度向右做匀速直线运动,当小物块运动到C点时,细绳被拉断.
如图所示,有一块平直的轻质木板(木板重力不计),其左端连接在转动轴O处,其右端A 用一根细绳系在竖直墙上的B 处,此时木板恰好水平,∠BAO=30°,细绳能承受的最大拉力为10N,OA两点间距是100cm.现将一个重为20N的物块(边长忽略不计)放在木板上O点处,让它在一个大小为8N的水平拉力作用下以2cm/s的速度向右做匀速直线运动,当小物块运动到C点时,细绳被拉断.