题目内容
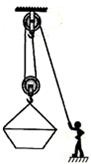 某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:(1)提升一次砖的最大重力;
(2)提升一次砖时滑轮组的最大机械效率;
(3)若全部完成提砖任务,工人利用此滑轮组至少做多少额外功.
分析:(1)根据滑轮组的结构确定承担物重的绳子股数,知道最大拉力和动滑轮重,利用F=
(G砖+G轮)求提升一次砖的最大重力;
(2)知道n=2,拉力移动的距离s=2h,分别求出有用和总功,利用效率公式求滑轮组的最大机械效率;
(3)求出了每次搬运砖的最大重力,求出搬运4000N需要的次数m,而每次搬运做的额外功W额=G轮h,据此求全部完成提砖任务,工人利用此滑轮组做的额外功.
| 1 |
| n |
(2)知道n=2,拉力移动的距离s=2h,分别求出有用和总功,利用效率公式求滑轮组的最大机械效率;
(3)求出了每次搬运砖的最大重力,求出搬运4000N需要的次数m,而每次搬运做的额外功W额=G轮h,据此求全部完成提砖任务,工人利用此滑轮组做的额外功.
解答:解:(1)由图知,使用滑轮组承担物重的绳子股数n=2,
∵滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计,
∴最大拉力:
F大=
×(G砖+G轮)=
×(G砖+100N)=500N,
∴提升一次砖的最大重力:
G砖=900N;
(2)提升一次砖时滑轮组的最大机械效率:
η大=
=
=
=
=90%;
(3)搬完4000N砖需要次数:
m=
≈4.4,需要5次搬完,
工人利用此滑轮组做额外功:
W额=G轮h×5=100N×4m×5=2000J.
答:(1)提升一次砖的最大重力为900N;
(2)提升一次砖时滑轮组的最大机械效率为90%;
(3)若全部完成提砖任务,工人利用此滑轮组至少做2000J的额外功.
∵滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计,
∴最大拉力:
F大=
| 1 |
| 2 |
| 1 |
| 2 |
∴提升一次砖的最大重力:
G砖=900N;
(2)提升一次砖时滑轮组的最大机械效率:
η大=
| W有 |
| W总 |
| Gh |
| F×2h |
| G |
| F×2 |
| 900N |
| 500N×2 |
(3)搬完4000N砖需要次数:
m=
| 4000N |
| 900N |
工人利用此滑轮组做额外功:
W额=G轮h×5=100N×4m×5=2000J.
答:(1)提升一次砖的最大重力为900N;
(2)提升一次砖时滑轮组的最大机械效率为90%;
(3)若全部完成提砖任务,工人利用此滑轮组至少做2000J的额外功.
点评:本题的关键有三:一是n的确定(直接从动滑轮上引出的绳子股数),二是不计摩擦和绳重时,W额=G轮h,三是不计摩擦和绳重时,F=
(G砖+G轮).
| 1 |
| n |

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
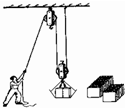 (2012?连云港二模)某建筑工地用如图所示的简易滑轮组将重3400N的砖块运到离地4m高的砌墙处.已知每个滑轮重100N,轮与轴的摩擦、绳重及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为400N,求:
(2012?连云港二模)某建筑工地用如图所示的简易滑轮组将重3400N的砖块运到离地4m高的砌墙处.已知每个滑轮重100N,轮与轴的摩擦、绳重及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为400N,求: (2012?太仓市一模)某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
(2012?太仓市一模)某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求: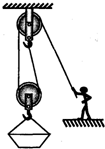 某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求: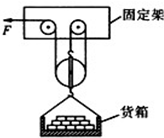 某建筑工地用如图所示升降机来提升实心砖.升降机货箱的重力是400N,每个滑轮中50N,不计钢丝绳的重力和摩擦.g取10N/kg.试求:
某建筑工地用如图所示升降机来提升实心砖.升降机货箱的重力是400N,每个滑轮中50N,不计钢丝绳的重力和摩擦.g取10N/kg.试求: