题目内容
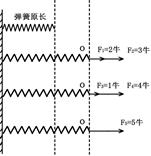
小明在“研究弹簧的伸长与外力的关系”的实验中，利用如图所示的装置，在弹簧下端分别挂不同个数的钩码（质量相等），使弹簧受到竖直向下的拉力，同时在刻度尺上读出每次弹簧下端指针的位置，将数据记录于下表．| 所受拉力F/N | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| 指针位置x/cm | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 5.8 | 5.8 |
| 弹簧的伸长x1/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 2.5 |
3 | 3.3 | 3.3 |
（2）分析表中实验数据，得到的结论是：
在弹性范围内，弹簧的伸长与外力成正比
在弹性范围内，弹簧的伸长与外力成正比
．（3）用题目中的弹簧制成弹簧测力计，其量程是
0～3
0～3
N．分析：（1）知道弹簧的原长和指针的位置，求出弹簧的伸长量．
（2）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，得出：在弹性范围内，弹簧的伸长与外力成正比．
（3）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，弹簧上挂钩码大于3N时，弹簧的伸长和拉力的比值不确定．
（2）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，得出：在弹性范围内，弹簧的伸长与外力成正比．
（3）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，弹簧上挂钩码大于3N时，弹簧的伸长和拉力的比值不确定．
解答：解：（1）由表格数据知，弹簧的原长是2.5cm，弹簧挂2.5N钩码时，指针指在5cm处，所以弹簧挂2.5N钩码时弹簧伸长5cm-2.5cm=2.5cm．
（2）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值是固定的，得出：在弹性范围内，弹簧的伸长与外力成正比．
（3）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，弹簧上挂钩码大于3N时，弹簧的伸长和拉力的比值不确定．用题目中的弹簧制成弹簧测力计量程是0～3N．
故答案为：（1）2.5；（2）在弹性范围内，弹簧的伸长与外力成正比；（3）0～3．
（2）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值是固定的，得出：在弹性范围内，弹簧的伸长与外力成正比．
（3）弹簧上挂钩码小于3N时，弹簧的伸长和拉力的比值一定，弹簧上挂钩码大于3N时，弹簧的伸长和拉力的比值不确定．用题目中的弹簧制成弹簧测力计量程是0～3N．
故答案为：（1）2.5；（2）在弹性范围内，弹簧的伸长与外力成正比；（3）0～3．
点评：弹簧的伸长和受到的拉力成正比条件是不能超过弹簧的弹性限度．
练习册系列答案
相关题目
（2012?徐汇区二模）为了研究弹簧受到拉力时，影响其长度增加量的有关因素，小明同学用测力计及一些不同的弹簧进行实验．如图所示，在实验中小明分别用力通过测力计拉伸不同的弹簧，测量并记录每根弹簧的原长、弹簧圈直径、长度增加量、所受拉力的大小等．记录数据如下列各表格所示，已知在同一表格中，实验所用弹簧的材料相同（即相同粗细的同种金属丝）．
阅读短文，回答问题。
无处不在的弹簧
弹簧在生活中随处可见，它在不同的领城发挥着重要作用。
弹簧的特点就是在拉伸或压缩时都要产生反抗外力作用的弹力，而且形变越大，产生的弹力越大；一旦外力消失，形变也消失。物理学家胡克研究得出结论：在弹性限度内，弹簧的形变量与它受到的拉力（或压力）成正比。
弹簧具有测量功能、紧压功能、复位功能和缓冲功能，以及储存能量的功能。弹簧在生产和生活中有许多应用，例如，制作弹簧侧力计、钢笔套上的夹片、机械钟表的发条等。
(1)弹簧被拉伸或压缩时都产生反抗外力作用的弹力，这说明 。
(2)胡克的结论是 。
(3）下表是小明研究弹簧长度与所受拉力大小关系时记录数据的表格，空格中的数据
是 。
|
钩码重/N |
0 |
0.5 |
1.0 |
|
2.0 |
2.5 |
|
弹簧长度/cm |
4 |
5 |
6 |
7 |
8 |
9 |
(4）举一个生活中应用弹簧的实例： 。（短文中实例除外）