题目内容
(2013?朝阳)小明是一位爱刨根问底的孩子,他和他几个同学在物理实验室里.想对弹簧测力计的工作原理一探究境.

探究一:测力计面板上的刻度为何是均匀的,他们打开测力计的外壳,发现内部结构如图丙,探究结果:弹簧的伸长量x与拉力F成正比关系,若设比例系数为k则F、k、x间的关系式可写为:
探究二:察看不同的测力计,如图甲与乙同样2N的拉力,甲的伸长量是乙的二倍,研究它们的内部结构发现,绕制甲弹簧的钢丝更细更柔软,结论:比例系数k与
探究三:他们联想到橡皮筋也近似符合弹簧的规律.那么,若将几根橡皮筋并排使用,更难拉伸,则他们整体的k要比一根橡皮筋的k要

探究一:测力计面板上的刻度为何是均匀的,他们打开测力计的外壳,发现内部结构如图丙,探究结果:弹簧的伸长量x与拉力F成正比关系,若设比例系数为k则F、k、x间的关系式可写为:
F=kx
F=kx
,并在丁图中用图象表示这种关系.探究二:察看不同的测力计,如图甲与乙同样2N的拉力,甲的伸长量是乙的二倍,研究它们的内部结构发现,绕制甲弹簧的钢丝更细更柔软,结论:比例系数k与
弹簧的粗细有关
弹簧的粗细有关
有关,k值小则意味着弹簧越容易拉伸
弹簧越容易拉伸
.探究三:他们联想到橡皮筋也近似符合弹簧的规律.那么,若将几根橡皮筋并排使用,更难拉伸,则他们整体的k要比一根橡皮筋的k要
大
大
(填“大”“小”或“相等”)分析:(1)根据弹簧的伸长量x与拉力F成正比关系,则x与F的比值是常数,设比例系数为k,便可得出F、k、x间的关系式;
正比例函数是一条过原点的直线,直线的斜率反映了比例系数k的值;
(2)若力相同,伸长量越大,力和伸长量的比值即比例系数k越小,说明弹簧越容易被拉长;
(3)根据(2)的分析,橡皮筋难拉伸,说明k值变大.
正比例函数是一条过原点的直线,直线的斜率反映了比例系数k的值;
(2)若力相同,伸长量越大,力和伸长量的比值即比例系数k越小,说明弹簧越容易被拉长;
(3)根据(2)的分析,橡皮筋难拉伸,说明k值变大.
解答:解:(1)因为弹簧的伸长量x与拉力F成正比关系,若设比例系数为k,则
=k,即F=kx;
则F与x的图象应为过原点的直线:
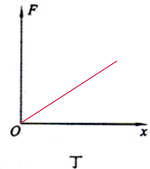
(2)根据F=kx,拉力均为2N,即F相等,甲的伸长量是乙的二倍,说明k甲=
;由题意知,绕制甲弹簧的钢丝更细更柔软,说明比例系数k与钢丝的粗细有关,k值小则弹簧更容易被拉伸;
(3)将几根橡皮筋并排使用,更难拉伸,说明整体的k要比一根橡皮筋的k大.
故答案为:
探究一:F=kx;
探究二:弹簧的粗细有关;弹簧越容易拉伸;
探究三:大.
| F |
| x |
则F与x的图象应为过原点的直线:

(2)根据F=kx,拉力均为2N,即F相等,甲的伸长量是乙的二倍,说明k甲=
| k乙 |
| 2 |
(3)将几根橡皮筋并排使用,更难拉伸,说明整体的k要比一根橡皮筋的k大.
故答案为:
探究一:F=kx;
探究二:弹簧的粗细有关;弹簧越容易拉伸;
探究三:大.
点评:此题是探究弹簧的伸长与拉力的正比例关系,通过分析得出比例系数得出F与x的关系,并通过实例分析,加深对k值的理解.

练习册系列答案
相关题目
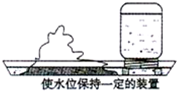 (2013?朝阳)小明假期要外出一段时间,她担心家里盆景中的水会因蒸发而干掉,于是用了一个塑料瓶装满水倒放在盆景景中,瓶口刚刚被水浸没,如图所示,这样就能使盆景中的水位保持一定的高度.下列说法正确的是( )
(2013?朝阳)小明假期要外出一段时间,她担心家里盆景中的水会因蒸发而干掉,于是用了一个塑料瓶装满水倒放在盆景景中,瓶口刚刚被水浸没,如图所示,这样就能使盆景中的水位保持一定的高度.下列说法正确的是( )