题目内容
 某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固 定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡,如果该同学身高160cm、质量为50kg,平躺到木板上后在托盘中再加上重为150N的物体,木板再次水平平衡.
某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固 定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡,如果该同学身高160cm、质量为50kg,平躺到木板上后在托盘中再加上重为150N的物体,木板再次水平平衡.(1)该装置中滑轮的作用是
改变力的方向
改变力的方向
(2)在测人体重心之前,先“在绳子末端的托盘上放一些重物,使木板水平平衡”,这样做的目的是
让木板先达到平衡状态,避免木板本身重力带来的实验误差
让木板先达到平衡状态,避免木板本身重力带来的实验误差
.(3)请在图中标注“杠杆的五要素”.
(4)请通过计算说明该同学的重心位置.(g取10N/kg )
分析:(1)定滑轮的工作特点是:不能省力,但能改变力的作用.
(2)此题可类比“杠杆平衡条件的探究实验”来进行分析,使木板水平平衡的目的主要有两方面:
①木板水平平衡时,可直接利用木板长,求出重心到支点O的距离(即:重心到头顶的长度),方便确定力臂;
②木板水平平衡时,可以排除木板自身重力对实验的影响.
(3)根据图示确定杠杆的支点、动力、动力臂、阻力、阻力臂等,并作图.
(4)木板处于水平平衡时,构成了以重物的重力为动力、木板长为动力臂、人的重力为阻力、重心到支点的距离为阻力臂的杠杆,其中,前两个条件都已给出,人的重力可由G=mg求得,直接根据杠杆的平衡条件代值计算,即可得出人的重心到支点O的距离,即重心到头顶的距离.
(2)此题可类比“杠杆平衡条件的探究实验”来进行分析,使木板水平平衡的目的主要有两方面:
①木板水平平衡时,可直接利用木板长,求出重心到支点O的距离(即:重心到头顶的长度),方便确定力臂;
②木板水平平衡时,可以排除木板自身重力对实验的影响.
(3)根据图示确定杠杆的支点、动力、动力臂、阻力、阻力臂等,并作图.
(4)木板处于水平平衡时,构成了以重物的重力为动力、木板长为动力臂、人的重力为阻力、重心到支点的距离为阻力臂的杠杆,其中,前两个条件都已给出,人的重力可由G=mg求得,直接根据杠杆的平衡条件代值计算,即可得出人的重心到支点O的距离,即重心到头顶的距离.
解答: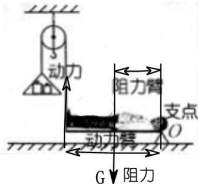 解:(1)由图可知,图示滑轮为定滑轮,木板左边的拉力方向向上,
解:(1)由图可知,图示滑轮为定滑轮,木板左边的拉力方向向上,
而重物的重力方向竖直向下,由此可见,定滑轮的作用是:改变力的方向;
(2)若在测量重心前不将杠杆调整为水平平衡,那么在测量过程中,
杠杆的阻力实际是人的重力与杠杆自重的和,这样就会影响到测量结果的准确性;
所以测量前,先在托盘上放置少量的重物,来平衡杠杆的自重,排除干扰.
这样做的目的是:让木板先达到平衡状态,避免木板本身重力带来的实验误差.
(3)杠杆的五要素如图所示.
(4)已知:G物=150N,L物=160cm=1.6m,G人=mg=50kg×10N/kg=500N;
由杠杆的平衡条件知:G物L物=G人L重,即:
L重=
=
=0.48m;
故答案为:(1)改变力的方向;(2)让木板先达到平衡状态,避免木板本身重力带来的实验误差;
(3)杠杆五要素如图所示;(4)该同学的重心位置为0.48m.
 解:(1)由图可知,图示滑轮为定滑轮,木板左边的拉力方向向上,
解:(1)由图可知,图示滑轮为定滑轮,木板左边的拉力方向向上,而重物的重力方向竖直向下,由此可见,定滑轮的作用是:改变力的方向;
(2)若在测量重心前不将杠杆调整为水平平衡,那么在测量过程中,
杠杆的阻力实际是人的重力与杠杆自重的和,这样就会影响到测量结果的准确性;
所以测量前,先在托盘上放置少量的重物,来平衡杠杆的自重,排除干扰.
这样做的目的是:让木板先达到平衡状态,避免木板本身重力带来的实验误差.
(3)杠杆的五要素如图所示.
(4)已知:G物=150N,L物=160cm=1.6m,G人=mg=50kg×10N/kg=500N;
由杠杆的平衡条件知:G物L物=G人L重,即:
L重=
| G物L物 |
| G人 |
| 150N×1.6m |
| 500N |
故答案为:(1)改变力的方向;(2)让木板先达到平衡状态,避免木板本身重力带来的实验误差;
(3)杠杆五要素如图所示;(4)该同学的重心位置为0.48m.
点评:此题考查了定滑轮的工作特点和杠杆平衡条件的综合应用,木板与同学的身高相同,是此题的一个隐含条件,需要注意.

练习册系列答案
相关题目
 (2008?义乌市)某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡.
(2008?义乌市)某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡.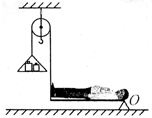 某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡.
某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡. 某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自已等长的木板,一端固定,另一端用轻质细绳通过一个滑轮组悬挂起(摩擦不计,动滑轮重不计)在绳子末端的托盘上放一些码砝,使木板水平平衡.如果该同学身高h,质量m1,平躺到木板上后在托盘中再加上质量为m2的码砝,木板再次水平平衡
某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自已等长的木板,一端固定,另一端用轻质细绳通过一个滑轮组悬挂起(摩擦不计,动滑轮重不计)在绳子末端的托盘上放一些码砝,使木板水平平衡.如果该同学身高h,质量m1,平躺到木板上后在托盘中再加上质量为m2的码砝,木板再次水平平衡 某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡.
某同学自制了一个可以测人体重心位置的装置,如图所示,取一块与自己等长的木板,一端固定,另一端用轻质细绳通过一个滑轮悬挂起来(摩擦不计),在绳子末端的托盘上放一些重物,使木板水平平衡.如果该同学身高160cm、质量40kg,平躺到木板上后在托盘中再加上重为137.2N的物体,木板再次水平平衡.