��Ŀ����
����Ŀ��������˼�����Сǿ������ȤС����ʵ���ң��¶�Ϊ20���������ۺ�ʵ�顣
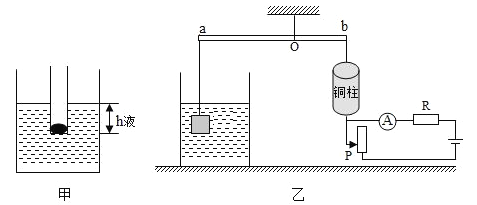
��1����С�����о����ܶȼƵĹ���ԭ������ͼ����ʾ���ܶȼƵļ�ģ�ͣ���һ����ϸ���ȵIJ������ڷ�һЩСǦ��ʹ������ֱƯ����Һ���У��貣���ܽ���Һ������ΪhҺ����Һ���ܶ�Ϊ��Һ���ܶȼ�Ư����ˮ��ʱ����ˮ�е����Ϊhˮ��ˮ���ܶ�Ϊ��ˮ�������Һ������hҺ��_____���ø�������������ʾ�����ɴ˿�֪�����ܶȼ�Ư����ú�ͣ��ܶ�Ϊ0.8��103kg/m3����ʱ�������hú����_____hˮ������ֵ�����ܶȼƿ̶��ص���_____��ѡ��ѡ��ǰ��Ţ���С�´� ���ϴ���С �۾��� ���������� ���������裩��
��2����С�������̽����ijҺ����ܶȺ��¶ȵĹ�ϵ�����������ͼ����ʾװ�ã���Ϊ0.6m�ľ�Ե���ʸܸ�ab�����ڸߴ�������O��ת�����ܸ�a�˵�����ϸ������һ���Ϊ1��10��3m3��ʵ�ĺϽ�飬��û���ձ��ڵ�Һ���С�b������ϸ�����ҵ�ͭ���������ƶ�ʱ�ܴ�����ƬP�ƶ�����ƬP������Ħ�����ơ�
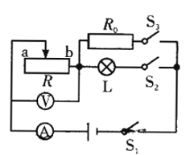
������Դ��ѹΪ3V������������������100�� 1A���������ڵ�·�д���һ������Ϊ0��15mA�ĵ�������Ϊ��֤��·��ȫ����ֵ����R����С��ֵ��_____����
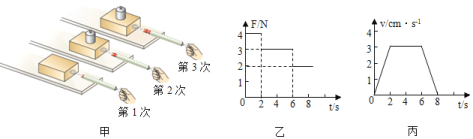
��Сǿ�ڸ���Һ����ȹ����з��֣�������ʾ����С����ɵó���Һ����ܶ����¶����߶�_____��ѡ����������������С�������������������ձ��ڵ�Һ���⣬װ������������������������Բ��ƣ��Ͻ��ʼ�ս�û����
��3����С�黹�����ô�װ�ü��������úϽ����ܶȡ���֪���ձ���Һ�����¶�Ϊ20��ʱ�Ƶ��ܶ�Ϊ1.1��103kg/m3���ܸ�ˮƽƽ��ʱ��ͭ������Ϊ2kg����O��ܸ�b��0.2m������ܶ���_____kg/m3����gȡ10N/kg��
���𰸡�![]() 1.25hˮ �� 200 ��С 2.1��103
1.25hˮ �� 200 ��С 2.1��103
��������
��һ�գ��ܶȼ���ˮ�к��ڱ���Һ���ж���Ư���ģ��ɸ���������֪�����������������Ը�����ȼ�Fˮ����FҺ��
�ɰ�����ԭ���ɵã�
��ˮgV��ˮ����ҺgV��Һ
��
��ˮgShˮ����ҺgShҺ
���ԣ��ܶȼƽ���Һ�����ȣ�
![]() ��
��
�ڶ��գ�ú�͵��ܶ�Ϊ����Һ��0.8��103kg/m3���ܶȼ�Ư����ú����ʱ�������Ϊ��
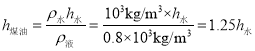 ��
��
�����գ���Ϊ��ˮgShˮ����ҺgShҺ�����ԣ���ˮhˮ����ҺhҺ��Һ���ܶȺͽ������ȳɷ��ȣ����Կ̶��Ǿ��ȵģ�
���Ŀգ�������������ֵΪ��ʱ����·�������ǣ�I��15mA��0.015A�����Զ�ֵ������С��ֵ��
![]() ��
��
����գ���ŷķ����![]() ֪��ѹ���䣬������ʾ����С�����·�ܵ�������˻�����������ֵ�����ͼ���֪��ʱ�ܸ��Ҷ������˶����ܸ�����³����Ͻ���ܵ��ĸ�����С���ɰ�����ԭ��
֪��ѹ���䣬������ʾ����С�����·�ܵ�������˻�����������ֵ�����ͼ���֪��ʱ�ܸ��Ҷ������˶����ܸ�����³����Ͻ���ܵ��ĸ�����С���ɰ�����ԭ��![]() ��֪��ûʱV�����䣬������С����Һ���ܶȱ�С�����ɵø�Һ����ܶ����¶����߶���С��
��֪��ûʱV�����䣬������С����Һ���ܶȱ�С�����ɵø�Һ����ܶ����¶����߶���С��
�����գ��Ͻ���ܵ��������������������ã��ܸ���ˮƽλ��ƽ�⣬�ɸܸ�ƽ������![]() �ɵã�
�ɵã�
��G�Ͻ���F������Oa��Gͭ��Ob������Ϊ�����û�������ſ�Һ�������������������ɵ� ��
����gV����ҺgV����Oa��mͭg��Ob
��
����V����ҺV������ab��Ob����mͭ��Ob
�������ݿɵ�:
������1��10��3m3��1.1��103kg/m3��1��10��3m3����(0.6m-0.2m)��2kg��0.2m��
������2.1��103kg/m3��