题目内容
某人把重100N的砂子提到6m高的楼上,桶重20N,人体重480N:
(1)人直接提着砂桶上楼,需要做的有用功是________J,额外功是________J,总功是________J机械效率是________.
(2)若人站在楼上,用重10N的动滑轮把上述砂桶提上楼,需要做的有用功是________J,额外功是________J,总功是________J,机械效率是________.
(3)若将(2)中的砂桶改用为重5N的口袋装砂子,则提砂子的过程中,需要做的有用功是________J,额外功是________J,总功是________J,机械效率是________.
解:三种情况下,有用功都是对砂子做的功,所以一样,
故W有用=Gh=100N×6m=600J
(1)额外功W额外1=G1h1=(20N+480N)×6m=3000J;
总功:W1=W有用+W额外1=600N+3000N=3600N;
机械效率 .
.
(2)额外功:W额外2=G2h2=(20N+10N)×6m=180J;
总功:W2=W有用+W额外2=600J+180J=780J;
机械效率: .
.
(3)额外功:W额外3=G3h3=(10N+5N)×6m=90J;
总功:W3=W有用+W额外3=600N+90N=690J;
机械效率: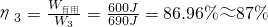 .
.
故答案为:(1)600,3000,3600,16.7%;
(2)600,180,780,76.9%;
(3)600,90,690,87%.
分析:有用功即克服重力做功,额外功即对滑轮、口袋、砂桶做的功,利用公式W=Gh三种情况一样;
总功即拉力做的功,利用公式W=FS计算.机械效率利用公式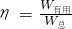 计算.
计算.
点评:通过本题的计算,我们知道做同样的有用功,所做的额外功越多,机械效率越低.
所以要提高机械效率,必须尽可能减少额外功.
故W有用=Gh=100N×6m=600J
(1)额外功W额外1=G1h1=(20N+480N)×6m=3000J;
总功:W1=W有用+W额外1=600N+3000N=3600N;
机械效率
 .
.(2)额外功:W额外2=G2h2=(20N+10N)×6m=180J;
总功:W2=W有用+W额外2=600J+180J=780J;
机械效率:
 .
.(3)额外功:W额外3=G3h3=(10N+5N)×6m=90J;
总功:W3=W有用+W额外3=600N+90N=690J;
机械效率:
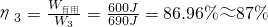 .
.故答案为:(1)600,3000,3600,16.7%;
(2)600,180,780,76.9%;
(3)600,90,690,87%.
分析:有用功即克服重力做功,额外功即对滑轮、口袋、砂桶做的功,利用公式W=Gh三种情况一样;
总功即拉力做的功,利用公式W=FS计算.机械效率利用公式
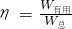 计算.
计算.点评:通过本题的计算,我们知道做同样的有用功,所做的额外功越多,机械效率越低.
所以要提高机械效率,必须尽可能减少额外功.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目