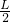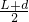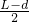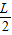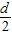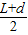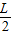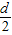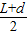题目内容
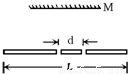
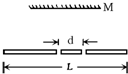 如图所示,一根长度为L的直薄木条上有两个观察小孔.两小孔之间的距离为d,d恰好是一个人两眼间的距离,当木条水平放置时,此人想通过两观察孔看见此木条在平面镜M里完整的像,那么选用的平面镜宽度至少是( )
如图所示,一根长度为L的直薄木条上有两个观察小孔.两小孔之间的距离为d,d恰好是一个人两眼间的距离,当木条水平放置时,此人想通过两观察孔看见此木条在平面镜M里完整的像,那么选用的平面镜宽度至少是( )分析:要使平面镜宽度CD最小,必须:左眼看的是C,右眼看的是A,根据平面镜成像特点以及光的反射定律,AM=BM,AO=BO,CQ=DQ,CN=DN,BD=AC,利用几何知识即可解答.
解答:解:用左眼看右边的,用右眼看左边的.如图所示:
(绿橙部分的长度即所求的平面镜宽度)
根据平面镜成像特点以及光的反射定律,
AM=BM,AO=BO,CQ=DQ,CN=DN,BD=AC,
由图可知,四边形BDAC为矩形,所以线段OQ=AE,则有:
OQ=AE=AC-EF-FC=L-d-FC,
又因为AE=FC,则OQ=
.
即平面镜宽度至少为OQ=
.
故选D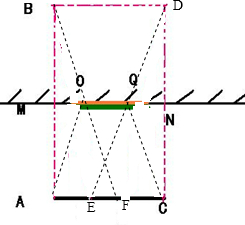
(绿橙部分的长度即所求的平面镜宽度)
根据平面镜成像特点以及光的反射定律,
AM=BM,AO=BO,CQ=DQ,CN=DN,BD=AC,
由图可知,四边形BDAC为矩形,所以线段OQ=AE,则有:
OQ=AE=AC-EF-FC=L-d-FC,
又因为AE=FC,则OQ=
| L-d |
| 2 |
即平面镜宽度至少为OQ=
| L-d |
| 2 |
故选D

点评:此题主要考查学生对平面镜成像的特点的理解和掌握,解答此题要结合几何知识,因此有一定的拔高难度,是一道竞赛题.

练习册系列答案
相关题目
 如图所示,一根均匀木尺放在水平桌面上,它的一端伸出桌面的外面,伸到桌面外面的部分长度是木尺长的1/4,在木尺末端的B点加一个作用力F,当力F=3牛时,木尺的另一端A开始向上翘起,那么木尺受到的重力为( )
如图所示,一根均匀木尺放在水平桌面上,它的一端伸出桌面的外面,伸到桌面外面的部分长度是木尺长的1/4,在木尺末端的B点加一个作用力F,当力F=3牛时,木尺的另一端A开始向上翘起,那么木尺受到的重力为( ) 如图所示,一根长度为L的直薄木条上有两个观察小孔.两小孔之间的距离为d,d恰好是一个人两眼间的距离,当木条水平放置时,此人想通过两观察孔看见此木条在平面镜M里完整的像,那么选用的平面镜宽度至少是
如图所示,一根长度为L的直薄木条上有两个观察小孔.两小孔之间的距离为d,d恰好是一个人两眼间的距离,当木条水平放置时,此人想通过两观察孔看见此木条在平面镜M里完整的像,那么选用的平面镜宽度至少是