题目内容
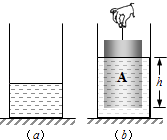
【题目】如图(a)所示,轻质薄壁圆柱形容器甲置于水平地面,底面积为3S,容器高0.25米,内盛0.15米深的水. 
(1)若容器的底面积为5×10﹣2米2 , 求容器中水的质量m.
(2)求0.05米深处水的压强p.
(3)现有面积为S、密度为6ρ水圆柱体乙,如图(b)所示,在乙上方沿水平方向切去高为△h的部分A(△h<0.3米),将A放入容器甲中(A与甲底部没有密合),并将此时的容器置于剩余圆柱体B的上方中央.
①若要使水对容器底部的压强p水最大,求切去部分A高度的最小值△h小 .
②求此时水对容器底部的压强p水与地面受到的压强p地的比值 ![]() .
.
【答案】
(1)解:水的体积V=Sh=5×10﹣2m2×0.15m=7.5×10﹣3m3,
由ρ= ![]() 得容器中水的质量:
得容器中水的质量:
m=ρV=1×103kg/m3×7.5×10﹣3m3=7.5kg;
(2)0.05米深处水的压强:
p=ρgh=1×103kg/m3×9.8N/kg×0.05m=49Pa;
(3)①若要使水对容器底部的压强p水最大,需要水深最大,排开水的体积:
V排=(0.25m﹣0.15m)×5×10﹣2m2=5×10﹣3m3,
则A的最小体积
VA=V排=5×10﹣3m3,
△h最小值:△h最小= ![]() =
=  =0.3m=30cm;
=0.3m=30cm;
②水对容器底部的压强最大压强:
p水=ρgh=0.25mρ水g;
当0.3m>△h≥0.25m时溢出的水最多、地面受到的压力最小,地面受到的压强最小:
p地= ![]() =
= ![]() =
= ![]() =2.2mρ水g,
=2.2mρ水g,
p水:p地=0.25m×ρ水g:2.2m×ρ水g=5:44= ![]() .
.
答:①切去部分A高度的最小值为30cm;②切去部分A高度0.3m>△h≥0.2m,比值为 ![]() .
.
【解析】(1)知道容器底面积和水深,求出水的体积,再利用m=ρV求水的质量;(2)知道深度,利用p=ρgh求水的压强;(3)①若要使水对容器底部的压强p水最大,需要水深最大,并且水不溢出,可求排开水的体积,即A的最小体积,进而求出△h最小值;
②水对容器底部的压强最大压强:p水=ρgh=0.25m×ρ水g;
地面受到的最小压力时,就是排出最多的水时,当A的高度大于容器的高就可以溢出最多的水,溢出水的体积等于容器的容积减去原来水的体积,则地面受到的最小压力等于乙的重力加上水的重力再减去溢出水的重,利用压强公式求出地面受到的最小压强,进而求出水对容器底部的压强p水与地面受到的压强p地的比值,此时最大.
【考点精析】根据题目的已知条件,利用压强的大小及其计算的相关知识可以得到问题的答案,需要掌握压强的计算公式及单位:公式:p =F/s ,p表示压强,F表示压力,S表示受力面积压力的单位是 N,面积的单位是 m2, 压强的单位是 N/m2,叫做帕斯卡,记作Pa .1Pa=1N/m2.(帕斯卡单位很小,一粒平放的西瓜子对水平面的压强大约为20Pa).