题目内容
 如图甲所示,重为900N的货物,放在水平地面上,与地面的接触面积为0.5m2
如图甲所示,重为900N的货物,放在水平地面上,与地面的接触面积为0.5m2(1)如图乙,一工人用滑轮组提升货物.10s内货物匀速上升了3m,则工人拉绳子的速度为多大?
(2)若动滑轮重G0=300N(不计绳重和摩擦),工人所用的拉力为多大?工人所做的功为多少?滑轮组的机械效率多大?
(3)若用该装置提起1200N的货物,那么货物上升3m,工人所做的功是多少?
分析:分析滑轮组,承担物重的绳子股数n=3,则s=3h.
(1)知道货物升高的高度,利用s=3h求绳子自由端移动的距离,利用速度公式求工人拉绳子的速度;
(2)不计绳重和摩擦,利用F=
(G物+G轮)求拉力大小,(1)中求出了绳子自由端移动的距离,利用W=Fs求工人所做的功;再利用W=Gh求出有用功,利用效率公式求滑轮组的机械效率;
(3)用该装置提起1200N的货物,不计绳重和摩擦,再利用F=
(G物+G轮)求拉力,知道货物上升高度,利用s=3h求出绳子自由端移动的距离,利用W=Fs求工人所做的功.
(1)知道货物升高的高度,利用s=3h求绳子自由端移动的距离,利用速度公式求工人拉绳子的速度;
(2)不计绳重和摩擦,利用F=
| 1 |
| 3 |
(3)用该装置提起1200N的货物,不计绳重和摩擦,再利用F=
| 1 |
| 3 |
解答:解:(1)绳子自由端移动的距离:
s=3h=3×3m=9m,
工人拉绳子的速度:
v=
=
=0.9m/s;
(2)∵不计绳重和摩擦,
∴F=
(G物+G轮)=
×(900N+300N)=400N,
工人所做的功:
W总=Fs=400N×9m=3600J;
工人所做的有用功:
W有用=Gh=900N×3m=2700J,
滑轮组的机械效率:
η=
×100%=
×100%=75%;
(3)用该装置提起1200N的货物,
F′=
(G′物+G轮)=
×(1200N+300N)=500N,
工人所做的功:
W′总=F′s=500N×9m=4500J.
答:(1)工人拉绳子的速度为0.9m/s;
(2)工人所用的拉力为400N;工人所做的功为3600J;滑轮组的机械效率75%;
(3)若用该装置提起1200N的货物,那么货物上升3m,工人所做的功是4500J.
s=3h=3×3m=9m,
工人拉绳子的速度:
v=
| s |
| t |
| 9m |
| 10s |
(2)∵不计绳重和摩擦,
∴F=
| 1 |
| 3 |
| 1 |
| 3 |
工人所做的功:
W总=Fs=400N×9m=3600J;
工人所做的有用功:
W有用=Gh=900N×3m=2700J,
滑轮组的机械效率:
η=
| W有用 |
| W总 |
| 2700J |
| 3600J |
(3)用该装置提起1200N的货物,
F′=
| 1 |
| 3 |
| 1 |
| 3 |
工人所做的功:
W′总=F′s=500N×9m=4500J.
答:(1)工人拉绳子的速度为0.9m/s;
(2)工人所用的拉力为400N;工人所做的功为3600J;滑轮组的机械效率75%;
(3)若用该装置提起1200N的货物,那么货物上升3m,工人所做的功是4500J.
点评:本题考查了学生对有用功、总功、机械效率的了解与掌握,利用好不计绳重和摩擦,拉力和物重的关系F=
(G物+G轮)是本题的关键.
| 1 |
| n |

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
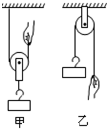
 小磊班的同学准备用如图甲所示的实验装置测量动滑轮的机械效率.
小磊班的同学准备用如图甲所示的实验装置测量动滑轮的机械效率.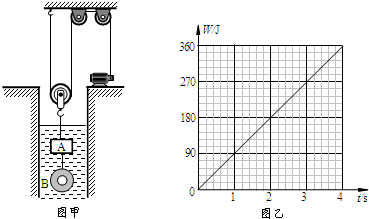
 (2011?思明区)如图甲所示,用动滑轮把重为100N的物体竖直匀速提高2m,滑轮重力为10N,不计绳重和摩擦,滑轮的机械效率是
(2011?思明区)如图甲所示,用动滑轮把重为100N的物体竖直匀速提高2m,滑轮重力为10N,不计绳重和摩擦,滑轮的机械效率是 如图甲所示,冰冻是造成高山地区冬季输配电线路倒塔(杆)断线的重要原因.为了避免这类事故的发生,一方面电力工人要及时对输电线路进行除冰作业,另一方面要加强输电线的抗拉能力.一般高压输电线每一根都是由一股位于中间的钢质线芯和六股相同粗细的铝质线芯绞在一起组成的,其横截面如图乙所示.这种输电线通常被称为钢芯铝绞线(代号LGJ).已知该钢芯铝绞线所能承受的最大安全拉力为其正常工作情况下拉力的5倍.下表是该种钢芯铝绞线的相关技术数据.
如图甲所示,冰冻是造成高山地区冬季输配电线路倒塔(杆)断线的重要原因.为了避免这类事故的发生,一方面电力工人要及时对输电线路进行除冰作业,另一方面要加强输电线的抗拉能力.一般高压输电线每一根都是由一股位于中间的钢质线芯和六股相同粗细的铝质线芯绞在一起组成的,其横截面如图乙所示.这种输电线通常被称为钢芯铝绞线(代号LGJ).已知该钢芯铝绞线所能承受的最大安全拉力为其正常工作情况下拉力的5倍.下表是该种钢芯铝绞线的相关技术数据.