题目内容
如图所示，轻质杠杆OA可绕O点转动，OA=0.3m，OB=0.2m，在A点处挂有一个质量为2Kg的物体G，在B点处加一个竖直向上的力F，杠杆在水平位置平衡，则物体G的重力为多少牛顿？力F为多少N？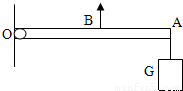
【答案】分析：已知物体的质量，由G=mg可以求出物体的重力，然后由杠杆平衡的条件求出力F的大小．
解答：解：物体的重力G=mg=2kg×9.8N/kg=19.6N；
由杠杆平衡的条件可得：
F×OB=G×OA，即F×0.2m=19.6N×0.3m，
解得：F=29.4N．
答：物体G的重力是19.6N，力F为29.4N．
点评：本题直接利用公式即可求解，属于基础性的考查，需注意计算时有单位，常数g在题干中未注明时取值为9.8N/kg．
解答：解：物体的重力G=mg=2kg×9.8N/kg=19.6N；
由杠杆平衡的条件可得：
F×OB=G×OA，即F×0.2m=19.6N×0.3m，
解得：F=29.4N．
答：物体G的重力是19.6N，力F为29.4N．
点评：本题直接利用公式即可求解，属于基础性的考查，需注意计算时有单位，常数g在题干中未注明时取值为9.8N/kg．
练习册系列答案
阅读快车系列答案
相关题目
21、如图所示，轻质杠杆可绕O转动，杠杆上吊一重物G，在力F作用下杠杆静止在水平位置，l为F的力臂，请在图中作出力F的示意图及重物G所受重力的示意图．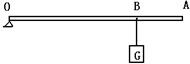
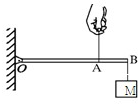（2011?金山区二模）如图所示，轻质杠杆OB可绕O点转动，OA的长0.3米，AB的长0.1米，B点处挂一个质量为3千克的物体M，A点处加一个竖直向上的力F，杠杆在水平位置平衡，则物体M的重力大小为
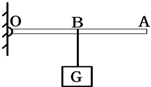如图所示，轻质杠杆OA可绕O点转动，杠杆长0.2米，在它的中点B处挂一重30牛的物体G．若在杠杆上A端施加最小的力F，使杠杆在水平位置平衡，画力F的方向并求出力F大小为多少牛？