【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
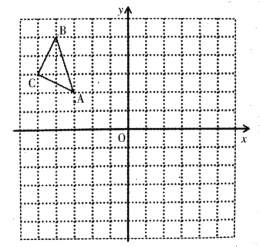
【题目】如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(﹣1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为 .

【题目】如图,⊙O的半径为2,弦AB的长为2![]() ,以AB为直径作⊙M,点C是优弧弧AB上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
,以AB为直径作⊙M,点C是优弧弧AB上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() -2 D. 4-2
-2 D. 4-2![]()