题目内容
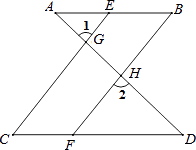
【题目】如图,在正方形ABCD中,点E为对角线AC上的一点,连接BE,DE.
(1)如图1,求证:△BCE≌△DCE;
(2)如图2,延长BE交直线CD于点F,G在直线AB上,且FG=FB.
①求证:DE⊥FG;
②已知正方形ABCD的边长为2,若点E在对角线AC上移动,当△BFG为等边三角形时,求线段DE的长。
【答案】(1)证明见解析;(2)①证明见解析;②DE=2(![]() ﹣1)
﹣1)
【解析】试题分析:(1)利用判定定理(SAS)可证;
(2)①利用(1)的结论与正方形的性质,只需证明∠FDE+∠DFG=90°即可;
②由DE⊥FG可构造直角三角形,利用等边三角形的性质及三角函数可求DE的长.
试题解析:(1)∵四边形ABCD是正方形,AC是其对角线,
∴∠DCE=∠BCE,CD=CB
在△BCE与△DCE中,

∴△BCE≌△DCE(SAS).
(2)①∵由(1)可知△BCE≌△DCE,
∴∠FDE=∠FBC
又∵四边形ABCD是正方形,
∴CD∥AB,
∴∠DFG=∠BGF,∠CFB=∠GBF,
又∵FG=FB,
∴∠FGB=∠FBG,
∴∠DFG=∠CFB,
又∵∠FCB=90°,
∴∠CFB+∠CBF=90°,
∴∠EDF+∠DFG=90°,
∴DE⊥FG
②如下图所示,
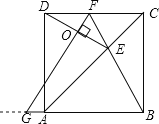
∵△BFG为等边三角形,
∴∠BFG=60°,
∵由(1)知∠DFG=∠CFB=60°,
在Rt△FCB中,∠FCB=90°,
∴FC=CBcot60°=![]() ,DF=2-
,DF=2-![]() ,
,
又∵DE⊥FG,
∴∠FDE=∠FED=30°,OD=OE,
在Rt△DFO中,
OD=DFcos30°=![]() -1,
-1,
∴DE=2(![]() -1)
-1)

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目