题目内容
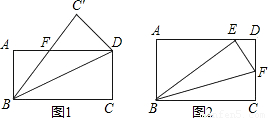
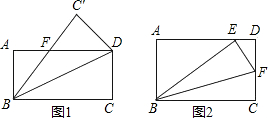 矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.(1)若AB=4,BC=8,求AF.
(2)若对折使C在AD上,AB=6,BC=10,求AE,DF的长.
分析:(1)如图1,由折叠的性质可证△ABF≌△C′DF,可得BF=DF,可判断重合部分为等腰三角形;设AF=x,则BF=DF=8-x,在Rt△ABF中,利用勾股定理可求AF;
(2)如图2,由折叠的性质可知BE=BC=10,又AB=6,在Rt△ABE中,由勾股定理可求AE,设DF=x,由折叠的性质得EF=FC=6-x,在Rt△DEF中,由勾股定理可求DF.
(2)如图2,由折叠的性质可知BE=BC=10,又AB=6,在Rt△ABE中,由勾股定理可求AE,设DF=x,由折叠的性质得EF=FC=6-x,在Rt△DEF中,由勾股定理可求DF.
解答:解:(1)如图1,由折叠的性质可知AB=CD=C′D,
又∠A=∠C′=90°,∠AFB=∠C′FD,
∴△ABF≌△C′DF,
∴BF=DF,
∴重合部分△BDF为等腰三角形;
设AF=x,则BF=DF=8-x,在Rt△ABF中,
由勾股定理得AB2+AF2=BF2,即42+x2=(8-x)2,
解得AF=x=3;
(2)如图2,由折叠的性质可知BE=BC=10,又AB=6,
在Rt△ABE中,由勾股定理,得AE=
=8;
设DF=x,由折叠的性质得EF=FC=6-x,DE=AD-AE=2,
在Rt△DEF中,由勾股定理得DE2+DF2=EF2,即22+x2=(6-x)2,
解得DF=x=
.
又∠A=∠C′=90°,∠AFB=∠C′FD,
∴△ABF≌△C′DF,
∴BF=DF,
∴重合部分△BDF为等腰三角形;
设AF=x,则BF=DF=8-x,在Rt△ABF中,
由勾股定理得AB2+AF2=BF2,即42+x2=(8-x)2,
解得AF=x=3;
(2)如图2,由折叠的性质可知BE=BC=10,又AB=6,
在Rt△ABE中,由勾股定理,得AE=
| BE2- AB2 |
设DF=x,由折叠的性质得EF=FC=6-x,DE=AD-AE=2,
在Rt△DEF中,由勾股定理得DE2+DF2=EF2,即22+x2=(6-x)2,
解得DF=x=
| 8 |
| 3 |
点评:本题考查了折叠的性质,三角形全等的判定与性质,勾股定理的运用.关键是根据折叠的性质将有关线段转化,把问题集中到直角三角形中解题.

练习册系列答案
相关题目
 4、红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )
4、红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )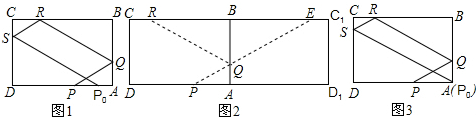
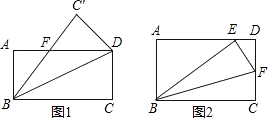 矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.