��Ŀ����
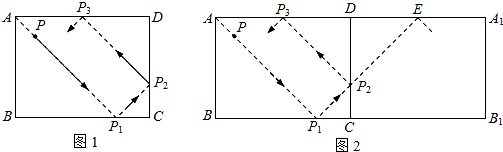
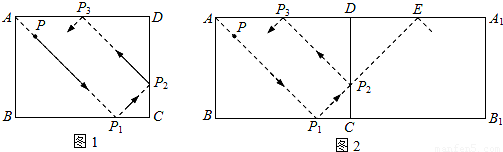
С������һ����Ȥ�����⣺������̨����ABCD�ı߳��ֱ�ΪAB=3��BC=5����P��AD�ϣ���AP=2��һ��ӵ�P������AD�н�Ϊ�ķ���������ֱ�ײ��AB��BC��CD��һ�κ��P0��ÿ��ײ������ʱ��ײ��ǰ���·�����������ɵĽ���ȣ�����ǵ��ڷ���ǣ�����ͼ����ʾ��С����˼����������ʼ�ģ���ͼ�ڣ�������ABCD��ֱ��AB�۵����õ�����ABC1D1������ԳƵ�֪ʶ������QE=QR��PE=PQ+QR��

����ο�С����˼·������Լ��ķ�������������⣺
��1������P0���P�غ�ʱ��������������·���ܳ���
��2������P0���A�غ�ʱ����ͼ�ۣ����������������·���ܳ��ȣ�
��3������P0�����߶�AP��ʱ����tan�ȵ�ȡֵ��Χ��

����ο�С����˼·������Լ��ķ�������������⣺
��1������P0���P�غ�ʱ��������������·���ܳ���
2
| 34 |
2
��| 34 |
��2������P0���A�غ�ʱ����ͼ�ۣ����������������·���ܳ��ȣ�
��3������P0�����߶�AP��ʱ����tan�ȵ�ȡֵ��Χ��
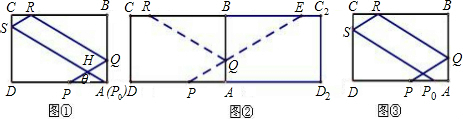
��������1��������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������P��PF��BC�ڵ�F�����ݷ���ǵ�������ǣ����жϡ�PER'�ǵ��������Σ����PE�ij��ȣ�����ȷ������·���ܳ��ȣ�
��2��������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������M��MN��AD�ڵ�N������
=
=
=
���ó�
=
=
������EF=3�����MN����Rt��PMN�����ù��ɶ������PM���̶��ɵó�PE��Ҳ�ɵó������˶���·�߳���
��3�����ݣ�1����2���ֱ�ȷ��tan�ȵ�ֵ���̶���ȷ������P0�����߶�AP��ʱ��tan�ȵ�ȡֵ��Χ��
��2��������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������M��MN��AD�ڵ�N������
| AP |
| ER�� |
| PM |
| ME |
| 2 |
| 10 |
| 1 |
| 5 |
| PM |
| PE |
| MN |
| EF |
| 1 |
| 6 |
��3�����ݣ�1����2���ֱ�ȷ��tan�ȵ�ֵ���̶���ȷ������P0�����߶�AP��ʱ��tan�ȵ�ȡֵ��Χ��
����⣺��1����ͼ��

������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������P��PF��BC�ڵ�F����ͼ1��ʾ��
������ɵã�CR=CR'��BR=BE��
��ER'=2BC=10��
������ǵ��ڷ���ǣ���RQ��PR'��
���ER'P=��ERQ��
���۵������ʿɵã���ERQ=��REQ��
���ER'Q=��REQ��
���PER'�ǵ��������Σ�
��EF=
ER'=5��
��Rt��EPF��EP=
=
��
�൱��P0���P�غ�ʱ��������������·���ܳ���=EP+PR'=2EP=2
��
��2����ͼ��

������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������M��MN��AD�ڵ�N����ͼ2��ʾ��
������ɵã�CR=CR'��BR=BE��
��ER'=2BC=10��
��AD��BC��
��
=
=
=
��
��
=
=
��
��EF=3��
��MN=
��
��PM=
=
��
��PE=3
��
�൱��P0���A�غ�ʱ��������������·���ܳ���=PE+AR'=2PE=6
��
��3���ɣ�1���ɵã�����P0���P�غ�ʱ��tan��=
��
�ɣ�2���ã�����P0���A�غ�ʱ��tan��=
��
���Ͽɵõ���P0�����߶�AP��ʱ��0.5��tan�ȡ�0.6��

������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������P��PF��BC�ڵ�F����ͼ1��ʾ��
������ɵã�CR=CR'��BR=BE��
��ER'=2BC=10��
������ǵ��ڷ���ǣ���RQ��PR'��
���ER'P=��ERQ��
���۵������ʿɵã���ERQ=��REQ��
���ER'Q=��REQ��
���PER'�ǵ��������Σ�
��EF=
| 1 |
| 2 |
��Rt��EPF��EP=
| PF2+EF2 |
| 34 |
�൱��P0���P�غ�ʱ��������������·���ܳ���=EP+PR'=2EP=2
| 34 |
��2����ͼ��

������ABCD��CD���ۣ��ҵ���R����CD�ĶԳƵ�R'������R'P������M��MN��AD�ڵ�N����ͼ2��ʾ��
������ɵã�CR=CR'��BR=BE��
��ER'=2BC=10��
��AD��BC��
��
| AP |
| ER�� |
| PM |
| ME |
| 2 |
| 10 |
| 1 |
| 5 |
��
| PM |
| PE |
| MN |
| EF |
| 1 |
| 6 |
��EF=3��
��MN=
| 1 |
| 2 |
��PM=
| PN2+MN2 |
| ||
| 2 |
��PE=3
| 5 |
�൱��P0���A�غ�ʱ��������������·���ܳ���=PE+AR'=2PE=6
| 5 |
��3���ɣ�1���ɵã�����P0���P�غ�ʱ��tan��=
| 3 |
| 5 |
�ɣ�2���ã�����P0���A�غ�ʱ��tan��=
| 1 |
| 2 |
���Ͽɵõ���P0�����߶�AP��ʱ��0.5��tan�ȡ�0.6��
�������������ڼ��α任���ۺ����⣬��Ҫ����Թ��ɶ��������ε����ʣ���Գ����ʣ���ֱ�������Σ����۱任��֪ʶ�����������գ����ۺ��������ʽ��������ǽ����Ĺؼ���ע����Ŀ��ʾ�Ľ��ⷽ����

��ϰ��ϵ�д�
�����Ŀ