Question

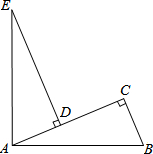
如图，在△ABC中，∠ACB=90º， D是AC上的一点，且AD=BC，DE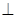AC于D，∠EAB=90º．
求证：AB=AE．

Answer 1

证明见解析.

试题分析：由垂直的性质就可以得出∠B=∠EAD，再根据AAS就可以得出△ABC≌△EAD，就可以得出AB=AE．
试题解析：∵∠EAB=90°，∴∠EAD+∠CAB=90°．
∵∠ACB=90°，∴∠B+∠CAB=90°．∴∠B=∠EAD．
∵ED⊥AC，∴∠EDA=90°．∴∠EDA=∠ACB．
在△ACB和△EDA中，∠B＝∠EAD，∠C＝∠EDA，BC＝AD，
∴△ACB≌△EDA（AAS），
∴AB=AE．