题目内容
(2012•三明)(1)解不等式组
并把解集在数轴上图1表示出来;
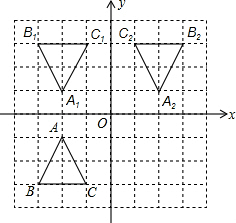
(2)如图2已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
①画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
②画出△ABC关于原点O对称的△A2B2C2,并写出点A2的坐标.

|
(2)如图2已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
①画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
②画出△ABC关于原点O对称的△A2B2C2,并写出点A2的坐标.

分析:(1)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可;
(2)①根据关于x轴对称的点的坐标特点画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
②根据关于原点对称的点的坐标特点画出△A2B2C2,并写出点A2的坐标.
(2)①根据关于x轴对称的点的坐标特点画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
②根据关于原点对称的点的坐标特点画出△A2B2C2,并写出点A2的坐标.
解答:解:(1)
解不等式①,得 x≤2,
解不等式②,得 x>-2,
故此不等式的解集为:-2<x≤2,
在数轴上表示为:

(2)①如图所示,A1(-2,1);
②如图所示,A2(2,1).
|
解不等式①,得 x≤2,
解不等式②,得 x>-2,
故此不等式的解集为:-2<x≤2,
在数轴上表示为:

(2)①如图所示,A1(-2,1);
②如图所示,A2(2,1).

点评:本题考查的是作图-旋转变换及轴对称变换,解一元一次不等式组及在数轴上表示不等式的解集,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
相关题目
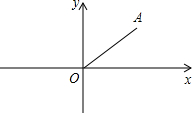 (2012•三明)如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
(2012•三明)如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )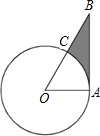 (2012•三明)如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )
(2012•三明)如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )