题目内容
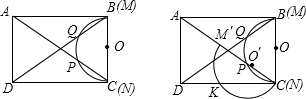
在矩形ABCD中,AD=2,2<AB<4,现将一个直径MN为2的量角器如图摆放,使其0°线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的度数分别是x、y.(1)求y与x之间的函数关系式(不必写出自变量的取值范围);
(2)将量角器绕C点逆时针旋转,使它的直径落在AC上,如图所示,O′为M′
 C的中点,此时量角器的半圆弧交DC于K,若K点的度数为z,那么z与y的数量关系是什么,请说明理由;
C的中点,此时量角器的半圆弧交DC于K,若K点的度数为z,那么z与y的数量关系是什么,请说明理由;(3)在(2)问图中,若M′B∥KO,求出此时AB的长.
分析:(1)由圆O和矩形ABCD是轴对称图形,得
=
=x°,因此
=180°-
,问题得解;
(2)连接O′K,∠KPC=180°-2∠PCK,∠PCK=90°-∠PCB,∠PCB=
∠POB=
(180°-x),由此问题得解;
(3)连接M′B、M′K、OK,证得四边形M′BOK为平行四边形,M′K=OB=1,再由△M′KC∽△ADC,求得CD,问题得证.
 |
| PC |
 |
| BQ |
 |
| CQ |
 |
| BQ |
(2)连接O′K,∠KPC=180°-2∠PCK,∠PCK=90°-∠PCB,∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)连接M′B、M′K、OK,证得四边形M′BOK为平行四边形,M′K=OB=1,再由△M′KC∽△ADC,求得CD,问题得证.
解答:解:(1)在⊙O中,
=
=x°,
∴
=180°-
,
即y=180°-x.
(2)z与y的数量关系是z=y.
理由:连接O′K,
由(1)知∠POB=∠COQ,
∴∠PCB=
∠POB=
(180°-x),
在矩形ABCD中,∠DCB=90°,
∴∠PCK=90°-∠ACB=
x,
又∵O′K=O′C,
∴∠PKC=∠PCK,
∴∠KPC=180°-2∠PCK=180°-x.
即
=
,z=y.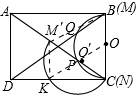
(3)如图
连接M′B、M′K、OK,
在⊙O′中,CM′为直径,
∴∠M′KC=90°,∠DCB=90°,
∴M′K∥BC,又M′B∥KO,
∴四边形M′BOK为平行四边形,
∴M′K=OB=1,
KC=
=
,
∵M′K∥AD,
∴△M′KC∽△ADC,
∴
=
,即
=
,CD=2
,
因此AB=CD=2
.
 |
| PC |
 |
| BQ |
∴
 |
| CQ |
 |
| BQ |
即y=180°-x.
(2)z与y的数量关系是z=y.
理由:连接O′K,
由(1)知∠POB=∠COQ,
∴∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
在矩形ABCD中,∠DCB=90°,
∴∠PCK=90°-∠ACB=
| 1 |
| 2 |
又∵O′K=O′C,
∴∠PKC=∠PCK,
∴∠KPC=180°-2∠PCK=180°-x.
即
 |
| CK |
 |
| CQ |

(3)如图
连接M′B、M′K、OK,
在⊙O′中,CM′为直径,
∴∠M′KC=90°,∠DCB=90°,
∴M′K∥BC,又M′B∥KO,
∴四边形M′BOK为平行四边形,
∴M′K=OB=1,
KC=
| CM′2- M′K2 |
| 3 |
∵M′K∥AD,
∴△M′KC∽△ADC,
∴
| KC |
| CD |
| M′K |
| AD |
| ||
| CD |
| 1 |
| 2 |
| 3 |
因此AB=CD=2
| 3 |
点评:本题主要运用圆心角、圆周角及它们之间的关系,平行四边形的判定与性质、相似三角形的判定与性质来解决问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( ) 如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围.
如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围. 如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF.
如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF. 在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE.
在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE. 如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.
如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.