题目内容
如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,则切线AB= cm.
【答案】分析:根据切线的性质知△OAB为直角三角形.在Rt△OBD中,可求出OB的长,然后在Rt△OAB中代入三角函数式可求AB的长.
解答:解:∵OA⊥BC,
∴根据垂径定理得:BD= BC=2.
BC=2.
在Rt△OBD中,∵∠AOB=60°,
∴OB=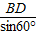 =
=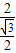 =
= ,
,
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∴AB=OB×tan∠AOB=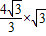 =4.
=4.
点评:本题主要考查的圆的切线性质,垂径定理和一些特殊三角函数值,有一定的综合性.
解答:解:∵OA⊥BC,
∴根据垂径定理得:BD=
 BC=2.
BC=2.在Rt△OBD中,∵∠AOB=60°,
∴OB=
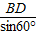 =
=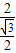 =
= ,
,∵AB与⊙O相切于点B,
∴∠ABO=90°.
∴AB=OB×tan∠AOB=
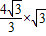 =4.
=4.点评:本题主要考查的圆的切线性质,垂径定理和一些特殊三角函数值,有一定的综合性.

练习册系列答案
相关题目

 9、如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=
9、如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=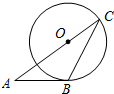 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=48°,则∠C=
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=48°,则∠C= 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.则sinA的值是
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.则sinA的值是 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C=
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C=