题目内容
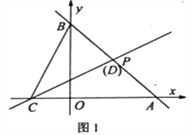
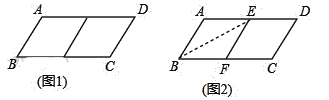
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
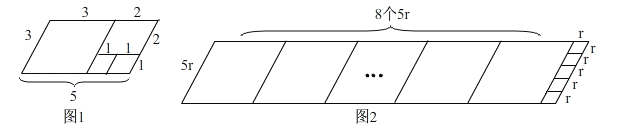
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
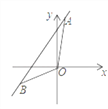
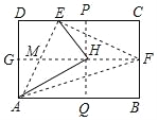
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
【答案】(1)3,12;(2)证明见解析.
【解析】试题分析:(1)利用平行四边形准菱形的意义即可得出结论;
(2)先判断出∠AEB=∠ABE,进而判断出AE=BF,即可得出结论.
试题解析:解:(1)如图1,利用邻边长分别为3和5的平行四边形进行3次操作,所剩四边形是边长为1的菱形,故邻边长分别为3和5的平行四边形是3阶准菱形:
如图2,∵b=5r,∴a=8b+r=40r+r=8×5r+r,利用邻边长分别为41r和5r的平行四边形进行8+4=12次操作,所剩四边形是边长为1的菱形,故邻边长分别为41r和5r的平行四边形是12阶准菱形:
故答案为:3,12.
(2)由折叠知:∠ABE=∠FBE,AB=BF,∵四边形ABCD是平行四边形,∴AE∥BF,∴∠AEB=∠FBE,∴∠AEB=∠ABE,∴AE=AB,∴AE=BF,∴四边形ABFE是平行四边形,∴四边形ABFE是菱形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1 | x=1,y=0 | x=3,y=2 | x=2,y=-1 | x=2,y=3 | |
A=2x-y | -3 | 2 | 4 | 5 | 1 |
B=4x2-4xy+y2 | 9 | 4 | 16 |
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.