题目内容
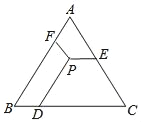
【题目】如图,三角形纸片ABC中,∠B=2∠C,把三角形纸片沿直线AD折叠,点B落在AC边上的E处,那么下列等式成立的是( )

A.AC=AD+BDB.AC=AB+BDC.AC=AD+CDD.AC=AB+CD
【答案】B
【解析】
根据题意证得AB=AE,BD=DE,DE=EC.据此可对以下选项进行一一判定.
∵△ADE是由△ADB沿直线AD折叠而成,∴AB=AE,BD=DE,∠B=∠AED.又∵∠B=2∠C,∠AED=∠C+∠EDC(三角形外角定理),∠EDC=∠C(等量代换),∴DE=EC(等角对等边).A、根据图示知:AC=AE+EC=AE+BD,则当AD≠AE时,AC≠AD+BD,A项错误;B、根据图示知,AC=AE+EC,因为AE+EC=AB+BD,所以AC=AB+BD,B项正确;C、在△ADC中,由三角形的三边关系可知AC<AD+CD,C项错误;D、根据图示知,AC=AE+EC,因为AE+EC=AB+BD,所以当EC≠CD时,AC≠AB+CD,D项错误.故选B.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目