题目内容
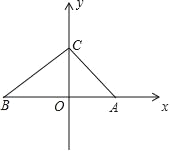
【题目】如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0）、（2，0）、（2，1）、（3，1）、（3，0）、（3，﹣1）、…，根据这个规律探索可得，第220个点的坐标为_____．
【答案】（21，2）．
【解析】
从图中可以看出横坐标为1的有一个点，横坐标为2的有2个点，横坐标为3的有3个点，…依此类推横坐标为n的有n个点．题目要求写出第220个点的坐标，我们可以通过加法计算算出第220个点位于第几列第几行，然后对应得出坐标规律，将行列数代入规律式．
解：在横坐标上，第一列有一个点，第二列有2个点…第n列有n个点，
并且奇数列点数对称而偶数列点数y轴上方比下方多一个，
∵1+2+3+…+20＝210，1+2+3+…+21＝231，
∴第220个点在第21列上，
所以奇数列的坐标为（n，
）（n，﹣1）…（n，
）；
偶数列的坐标为（n，
）（n，﹣1）…（n，1﹣），
由加法推算可得到第220个点位于第21列自下而上第12行．
第21列一共有21个点，上下对称，x轴上有一个，x轴上方和下方各10个点，
∴第220个点的坐标为（21，2），
故答案为（21，2）．
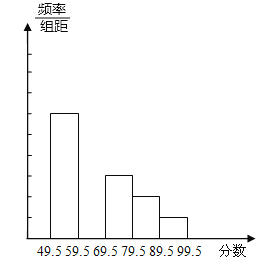
【题目】学校为了解全校
名学生双休日在家最爱选择的电视频道情况，问卷要求每名学生从“新闻，体育，电影，科教，其他”五项中选择其一，随机抽取了部分学生，调查结果绘制成未完成的统计图表如下：
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
求调查的学生人数及统计图表中
的值；
求选择其他频道在统计图中对应扇形的圆心角的度数；
求全校最爱选择电影频道的学生人数.
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A、B、C、D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
（1）表中的a=________，b=________；
（2）根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；
（3）若该校有学生1000名，根据调查结果估计该校学生中类别为C的人数约为多少？
