题目内容
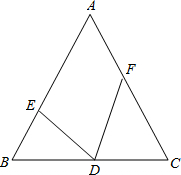 如图,△ABC中,AB=AC=5,BC=6,点D是BC的中点,∠EDF=∠B,点E、F分别在AB、AC上.
如图,△ABC中,AB=AC=5,BC=6,点D是BC的中点,∠EDF=∠B,点E、F分别在AB、AC上.(1)证明△BED∽△CDF;
(2)设BE=x,CF=y,求y与x的函数关系式,并写出x的取值范围;
(3)连EF,△DEF能否成为等腰三角形?如果可能,求出相应的x的值.
分析:(1)由平角的定义得到∠EDB+∠FDC=180°-∠EDF,利用三角形的内角和定理得到∠DEB+∠EDB=180°-∠B,再由∠EDF=∠B,利用等量代换得到一对角相等,再由AB=AC,利用等边对等角得到一对角相等,利用两对应角相等的两三角形相似可得证;
(2)由(1)得到的三角形相似,利用相似得比例,将各自的值代入列出y关于x的函数关系式,并求出x的范围即可;
(3)△DEF能成为等腰三角形,理由为:当BE=CF时,利用SAS可得出三角形BED和三角形CFD全等,由全等三角形的对应边相等可得出DE=DF,即三角形DEF为等腰三角形,此时y=x,代入由(2)得出的函数解析式,列出关于x的方程,求出方程的解即可得到x的值.
(2)由(1)得到的三角形相似,利用相似得比例,将各自的值代入列出y关于x的函数关系式,并求出x的范围即可;
(3)△DEF能成为等腰三角形,理由为:当BE=CF时,利用SAS可得出三角形BED和三角形CFD全等,由全等三角形的对应边相等可得出DE=DF,即三角形DEF为等腰三角形,此时y=x,代入由(2)得出的函数解析式,列出关于x的方程,求出方程的解即可得到x的值.
解答:解:(1)证明:∵∠EDB+∠FDC=180°-∠EDF,∠DEB+∠EDB=180°-∠B,且∠EDF=∠B,
∴∠FDC=∠DEB,
又AB=AC,∴∠B=∠C,
∴△BED∽△CDF;
(2)∵△BED∽△CDF,
∴
=
=
,
∵AB=AC=5,BC=6,点D是BC的中点,
∴BD=CD=3,又BE=x,CF=y,
∴
=
,
则y=
(0<x<5);
(3)△DEF能成为等腰三角形,理由为:
若BE=CF,
在△BED和△CFD中,
,
∴△BED≌△CFD(SAS),
∴DE=DF,即△DEF能成为等腰三角形,
此时y=x,即
=x,
解得:x=3或x=-3(舍去),
则当x=3时,△DEF为等腰三角形.
∴∠FDC=∠DEB,
又AB=AC,∴∠B=∠C,
∴△BED∽△CDF;
(2)∵△BED∽△CDF,
∴
| BE |
| CD |
| ED |
| DF |
| BD |
| CF |
∵AB=AC=5,BC=6,点D是BC的中点,
∴BD=CD=3,又BE=x,CF=y,
∴
| x |
| 3 |
| 3 |
| y |
则y=
| 9 |
| x |
(3)△DEF能成为等腰三角形,理由为:
若BE=CF,
在△BED和△CFD中,
|
∴△BED≌△CFD(SAS),
∴DE=DF,即△DEF能成为等腰三角形,
此时y=x,即
| 9 |
| x |
解得:x=3或x=-3(舍去),
则当x=3时,△DEF为等腰三角形.
点评:此题属于相似形综合题,涉及的知识有:全等三角形的判定与性质,以及相似三角形的判定与性质,利用了转化及等量代换的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.