题目内容
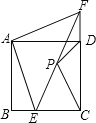
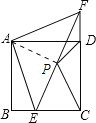
【题目】如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(1)求证:AE=AF;
(2)若∠AEB=75°,求∠CPD的度数.
【答案】(1)证明见解析;(2)105°.
【解析】
试题
(1)由已知条件证△ABE≌△ADF即可可得到AE=AF;
(2)
试题解析:
(1)∵四边形ABCD为正方形,
∴∠B=∠ADC=∠ADF=90°,AB=AD,
又∵BE=DF,
∵在△ABE和△ADF中,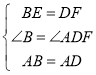 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)连结AP,
∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
又∵AE=AF,
∴∠AEF=45°,
∵∠AEB=75°,
∴∠CEF=180°﹣45°﹣75°=60°,
∴∠EFC=180°-90°-60°=30°,
∵∠ECF=90°,P为EF中点,
∴CP=PF=![]() EF,
EF,
∴∠EFC=∠PCF=30°,
∵P为EF中点,∠EAF=90°,
∴AP=![]() EF,
EF,
∴AP=CP,
∵在△APD和△CPD中: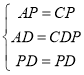 ,
,
∴△APD≌△CPD(SSS),
∴∠ADP=∠CDP=![]() ∠ADC=45°,
∠ADC=45°,
∴∠CPD=180°﹣∠PCD﹣∠CDP=105°.

练习册系列答案
相关题目