题目内容
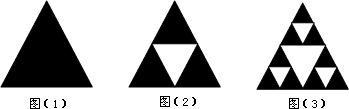
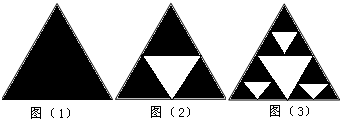
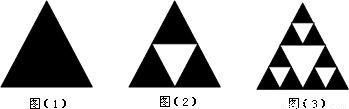
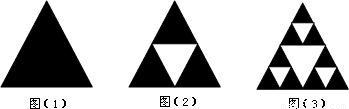
图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是______.

解:设白三角形x个,黑三角形y个,
则:n=1时,x=0,y=1;
n=2时,x=0+1=1,y=3;
n=3时,x=3+1=4,y=9;
n=4时,x=4+9=13,y=27;
当n=5时,x=13+27=40,
所以白的正三角形个数为:40,
故答案为:40.
分析:本题可根据图形,可知后一个三角形中白三角形的个数=前一个三角形的白三角形个数加上黑三角形个数.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
则:n=1时,x=0,y=1;
n=2时,x=0+1=1,y=3;
n=3时,x=3+1=4,y=9;
n=4时,x=4+9=13,y=27;
当n=5时,x=13+27=40,
所以白的正三角形个数为:40,
故答案为:40.
分析:本题可根据图形,可知后一个三角形中白三角形的个数=前一个三角形的白三角形个数加上黑三角形个数.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目