题目内容
若25个数据的平均数是4,方差是5,则这组数据的平方和为________.
525
分析:设这组数据的平方和为x,根据方差的公式即方差S2= [x12+x22+…+xn2]-
[x12+x22+…+xn2]- 2代入计算即可.
2代入计算即可.
解答:设这组数据的平方和为x,
∵25个数据的平均数是4,方差是5,
∴ x-42=5,
x-42=5,
解得:x=525,
则这组数据的平方和为525;
故答案为:525.
点评:本题考查了方差的计算.一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2=
,则方差S2= [x12+x22+…+xn2]-
[x12+x22+…+xn2]- 2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
分析:设这组数据的平方和为x,根据方差的公式即方差S2=
 [x12+x22+…+xn2]-
[x12+x22+…+xn2]- 2代入计算即可.
2代入计算即可.解答:设这组数据的平方和为x,
∵25个数据的平均数是4,方差是5,
∴
 x-42=5,
x-42=5,解得:x=525,
则这组数据的平方和为525;
故答案为:525.
点评:本题考查了方差的计算.一般地设n个数据,x1,x2,…xn的平均数为
 ,则方差S2=
,则方差S2= [x12+x22+…+xn2]-
[x12+x22+…+xn2]- 2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 
练习册系列答案
相关题目
2011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
| 分组 | 频数 | 频率 | |
| 一组 | 0 | 0 | 0 |
| 二组 | 5 | 10 | 0.10 |
| 三组 | 10 | 10 |
|
| 四组 | 15 |
| 0.50 |
| 五组 | 20 | 30 | 0.30 |
| 合计 | 100 | 1.00 |
(1)在表中填写缺失的数据;
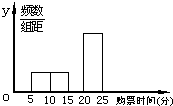
(2)画出频数分布直方图;
(3)求购票时间的平均数
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么 决策一下至少要增加几个窗口?
2011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
|
分组 |
频数 |
频率 |
|
|
一组 |
0 |
0 |
0 |
|
二组 |
5 |
10 |
0.10 |
|
三组 |
10 |
10 |
|
|
四组 |
15 |
|
0.50 |
|
五组 |
20 |
30 |
0.30 |
|
合计 |
100 |
1.00 |
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)求购票时间的平均数
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么 决策一下至少要增加几个窗口?
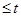 <5
<5