题目内容
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() .
.

(1)若![]() 是
是![]() 的高线,且
的高线,且![]() ,求
,求![]() 的长.
的长.

(2)若![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求出
,求出![]() 的面积.
的面积.

(3)填空:若![]() 是
是![]() 的中线,设
的中线,设![]() 长为
长为![]() ,则
,则![]() 的取值范围______.
的取值范围______.

【答案】(1)![]() ;(2)
;(2)![]() 的面积为
的面积为![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 相交于点
相交于点![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,根据
,根据![]() 即可求得BC的长;(2)过点
即可求得BC的长;(2)过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 交于点
交于点![]() ,根据角平分线的性质定理可得
,根据角平分线的性质定理可得![]() ,设
,设![]() ,根据三角形的面积公式,结合已知条件可得
,根据三角形的面积公式,结合已知条件可得![]() ,解方程求得
,解方程求得![]() ,由此即可求得
,由此即可求得![]() 的面积;(3)延长AD至点E,使DE=AD,连接EC,先证明△ABD≌△ECD,在△AEC中,由三角形的三边关系定理即可求解.
的面积;(3)延长AD至点E,使DE=AD,连接EC,先证明△ABD≌△ECD,在△AEC中,由三角形的三边关系定理即可求解.
(1)过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 相交于点
相交于点![]()
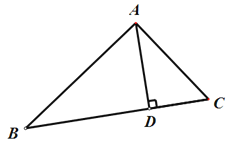
在![]() 中,由勾股定理得
中,由勾股定理得![]()
在![]() 中,由勾股定理得
中,由勾股定理得![]()
![]()
综上所述:![]() .
.
(2)过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 交于点
交于点![]() ,
,
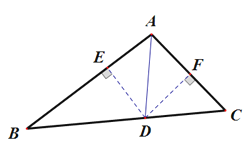
![]() 是
是![]() 的角平分线
的角平分线
![]()
![]()
设![]()
![]()
∴解得![]()
![]()
综上所述:![]() 的面积为
的面积为![]()
(3)延长AD至点E,使DE=AD,连接EC,
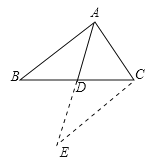
∵BD=CD,DE=AD,∠ADB=∠EDC,
∴△ABD≌△ECD,
∴CE=AB,
∵AB= CE=4,AC=3,
设AD=m,则AE=2m,
∴4-3<2m<4+3,
∴0.5<m<3.5,
故答案为:0.5<m<3.5.

【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量![]() (万件)是销售单价
(万件)是销售单价![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价![]() 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价![]() 的范围).
的范围).