题目内容
已知圆锥的侧面积为16πcm2.(1)求圆锥的母线长L(cm)关于底面半径r(cm)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
【答案】分析:(1)根据圆锥的底面周长等于圆锥侧面展开扇形的弧长,用圆锥的底面半径和母线长表示出其侧面积就能得到;
(2)根据底面半径小于其母线长且大于零确定底面半径的取值范围;
(3)根据圆锥的侧面积和其圆心角的度数求出其母线长,然后利用勾股定理求圆锥的高.
解答:解:(1)∵S=πrL=16π,
∴L=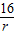 ;
;
(2)∵L=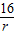 >r>0,
>r>0,
∴0<r<4;
(3)∵θ=90°=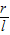 ×3600,
×3600,
∴L=4r,
又L=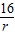 ,
,
∴r=2,
∴L=8,
∴h=2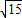 .
.
点评:本题考查了圆锥的侧面积与圆锥的底面积之间的相互转化,二者通过圆锥的母线、圆锥的底面周长与圆锥的侧面展开扇形的弧长建立关系.
(2)根据底面半径小于其母线长且大于零确定底面半径的取值范围;
(3)根据圆锥的侧面积和其圆心角的度数求出其母线长,然后利用勾股定理求圆锥的高.
解答:解:(1)∵S=πrL=16π,
∴L=
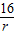 ;
;(2)∵L=
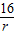 >r>0,
>r>0,∴0<r<4;
(3)∵θ=90°=
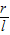 ×3600,
×3600,∴L=4r,
又L=
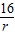 ,
,∴r=2,
∴L=8,
∴h=2
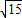 .
.点评:本题考查了圆锥的侧面积与圆锥的底面积之间的相互转化,二者通过圆锥的母线、圆锥的底面周长与圆锥的侧面展开扇形的弧长建立关系.

练习册系列答案
相关题目
已知圆锥的侧面积为15πcm2,底面半径为3cm,则圆锥的高是( )
| A、3cm | B、4cm | C、5cm | D、8cm |
已知圆锥的侧面积为8πcm2,侧面展开图的圆心角为45°,则该圆锥的母线长为( )
| A、64cm | ||||
| B、8cm | ||||
| C、2cm | ||||
D、
|