题目内容
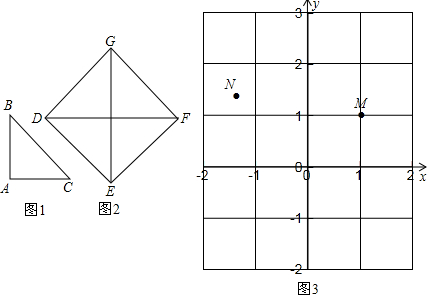
已知:如图1,△ABC是直角三角形,AB=AC=1,用四个与△ABC全等的三角形拼成一个正方形DEFG,如图2.
(1)正方形的DEFG的面积是
;
(2)△ABC的斜边BC长=
;
(3)根据上面的经验解决问题:直角坐标系中,M(1,1),N(-
,
),点P在x轴上,则PM+PN的最小值是
+2
+2,并在图中作出点P.
(1)正方形的DEFG的面积是
2
2
,正方形的DEFG的边长是| 2 |
| 2 |
(2)△ABC的斜边BC长=
| 2 |
| 2 |
(3)根据上面的经验解决问题:直角坐标系中,M(1,1),N(-
| 2 |
| 2 |
| 2 |
| 2 |

分析:(1)利用直角三角形的面积求法以及正方形面积得出即可;
(2)利用勾股定理得出斜边长即可;
(3)作出M点关于x轴的对称点,进而连接NM′,与x轴交点即是P点,再利用构造直角三角形利用勾股定理得出即可.
(2)利用勾股定理得出斜边长即可;
(3)作出M点关于x轴的对称点,进而连接NM′,与x轴交点即是P点,再利用构造直角三角形利用勾股定理得出即可.
解答: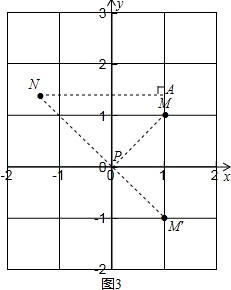 解:(1)∵△ABC是直角三角形,AB=AC=1,
解:(1)∵△ABC是直角三角形,AB=AC=1,
∴△ABC的面积为:
×1×1=
,
∴用四个与△ABC全等的三角形拼成一个正方形DEFG面积是:4×
=2;
∴正方形的DEFG的边长是:
;
故答案为:2,
;
(2)∵△ABC是直角三角形,AB=AC=1,
∴△ABC的斜边长为:
;
故答案为:
;
(3)如图所示:点P即为所求,
过点N作NA⊥MM′于点A,
∵M(1,1),N(-
,
),
∴AN=
+1,AM′=
+1,
∴NM′=
(
+1)=2+
,
∴PM+PN的最小值是:
+2.
故答案为:
+2.
 解:(1)∵△ABC是直角三角形,AB=AC=1,
解:(1)∵△ABC是直角三角形,AB=AC=1,∴△ABC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
∴用四个与△ABC全等的三角形拼成一个正方形DEFG面积是:4×
| 1 |
| 2 |
∴正方形的DEFG的边长是:
| 2 |
故答案为:2,
| 2 |
(2)∵△ABC是直角三角形,AB=AC=1,
∴△ABC的斜边长为:
| 2 |
故答案为:
| 2 |
(3)如图所示:点P即为所求,
过点N作NA⊥MM′于点A,
∵M(1,1),N(-
| 2 |
| 2 |
∴AN=
| 2 |
| 2 |
∴NM′=
| 2 |
| 2 |
| 2 |
∴PM+PN的最小值是:
| 2 |
故答案为:
| 2 |
点评:此题主要考查了勾股定理的应用以及利用对称点求最小值问题,根据已知得出P点位置是解题关键.

练习册系列答案
相关题目
 已知,如图,DC∥AB,且DC=
已知,如图,DC∥AB,且DC= 12、已知:如图,CD∥AB,∠A=40°,∠B=60°,那么∠1=
12、已知:如图,CD∥AB,∠A=40°,∠B=60°,那么∠1=
 17、已知:如图,CE⊥AB,DF⊥AB,AF=BE,CE=DF.
17、已知:如图,CE⊥AB,DF⊥AB,AF=BE,CE=DF.