��Ŀ����
����Ŀ��ijУ�ڻ��زμ����ʵ�������У�������ʦ����ѧ�������ؼƻ��½�һ�����ε������أ�һ�߿���ǽ��ǽ�㹻�����������������ܳ�37���IJ����դ��Χ�ɣ���ǽƽ�е�һ����һ����Ϊ3���ij���ڣ���ͼ��ʾ�������Ʋ���ʹ�ص���������ͼ����λѧ��������龳��������������Ϣ��������⣺
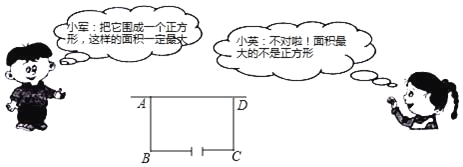
��1����AB=x�ף�x��0�������ú�x�Ĵ���ʽ��ʾBC�ij���
��2�������ж�˭��˵����ȷ��Ϊʲô��
���𰸡���1��BC=37+3��2x=40��2x
��2��СӢ˵����ȷ��ԭ�������
��������
����������������κ������ʵ�����⣮������ȷ���Ա���ȡֵ��ΧʱҪ�����Ŀ�е�ͼ�κͳ�������ԭ���ҵ�����x�IJ���ʽ��
��1����AB=x�ף����ݵ�ʽx+x+BC=37+3���������BC�ı���ʽ��
��2���ó������ϵʽ�����������ϵʽ�����жϼ��ɣ�
�⣺��1����AB=x�ף��ɵã�BC=37+3��2x=40��2x��
��2��СӢ˵����ȷ��
�������S=x��40��2x��=��2��x��10��2+200��
����x=10ʱ��Sȡ���ֵ��
��ʱx��40��2x����������IJ��������Σ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ