题目内容
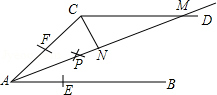
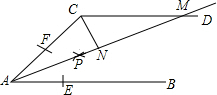 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E、F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E、F为圆心,大于| 1 | 2 |
分析:根据AB∥CD,∠ACD=120°,得出∠CAB=60°,再根据AM是∠CAB的平分线,即可得出∠MAB的度数.
解答:解:∵AB∥CD,
∴∠ACD+∠CAB=180°,
又∵∠ACD=120°,
∴∠CAB=60°,
由作法知,AM是∠CAB的平分线,
∴∠MAB=
∠CAB=30°.
故答案为:30°.
∴∠ACD+∠CAB=180°,
又∵∠ACD=120°,
∴∠CAB=60°,
由作法知,AM是∠CAB的平分线,
∴∠MAB=
| 1 |
| 2 |
故答案为:30°.
点评:此题考查了作图-复杂作图,用到的知识点是平行线的性质、角平分线的性质等,解题的关键是得出∠MAB=
∠CAB.
| 1 |
| 2 |

练习册系列答案
相关题目
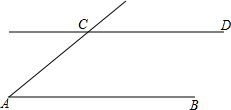 (2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于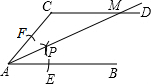 如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于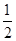 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。