题目内容
下列命题中,真命题为( )A.对角线相等的四边形一定是矩形
B.底角相等的两个等腰三角形一定全等
C.平行四边形的一条对角线分成的两个三角形一定相似
D.有公共顶点和一条公共边的两角,若其和为180°,则这两角互为邻补角
【答案】分析:根据矩形、等腰三角形、相似三角形的判断和邻补角的定义分别对每一项进行分析即可.
解答:解:A、对角线相等的四边形不一定是矩形,故本选项是假命题;
B、底角相等的两个等腰三角形不一定全等,故本选项是假命题;
C、平行四边形的一条对角线分成的两个三角形一定相似,故本选项是真命题;
D、有公共顶点和一条公共边的两角,若其和为180°,则这两角不一定互为邻补角,故本选项是假命题;
故选C.
点评:此题考查了命题与定理,解题的关键是掌握正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假需要熟悉课本中的性质定理.
解答:解:A、对角线相等的四边形不一定是矩形,故本选项是假命题;
B、底角相等的两个等腰三角形不一定全等,故本选项是假命题;
C、平行四边形的一条对角线分成的两个三角形一定相似,故本选项是真命题;
D、有公共顶点和一条公共边的两角,若其和为180°,则这两角不一定互为邻补角,故本选项是假命题;
故选C.
点评:此题考查了命题与定理,解题的关键是掌握正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假需要熟悉课本中的性质定理.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
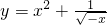 图象上的点P(x,y)一定在第二象限
图象上的点P(x,y)一定在第二象限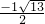 .
.