��Ŀ����
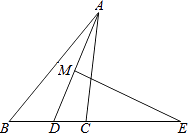
����Ŀ����ͼ1����ABC�ı�BC��ֱ��l�ϣ�AC��BC����AC=BC����EFP�ı�FPҲ��ֱ��l�ϣ���EF���AC�غϣ���EF=FP��
��1��ֱ��д��AB��AP�������������ϵ��_____��AB��AP��λ�ù�ϵ��_____��
��2������ABC��ֱ��l����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ����֤��AP=BQ��
��3������ABC��ֱ��l����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ����̽��AP=BQ�Ƿ��Գ�������˵�����ɣ�

���𰸡���1��AB=AP��AB��AP����2��֤������������3�����������ɼ�����.
�������������������1��AB=AP��AB��AP����֪AC��BC��AC=BC���ɵ���ABCΪ����ֱ�������Σ�������BAC=��ABC=45����������֪������֤��PEF=45�������ɵ���BAP=90�������۵�֤����2��������֪������֤Rt��BCQ��Rt��ACP������ȫ�������ε����ʼ��ɵý�������3�������Գ�������ȣ�2������֤�����ɣ�
���������
��1��AB=AP��AB��AP��
֤������AC��BC��AC=BC��
���ABCΪ����ֱ�������Σ�
���BAC=��ABC=![]() ��180�㩁��ACB��=45����
��180�㩁��ACB��=45����
��֪����ABC�ա�EFP��
ͬ����֤��PEF=45����
���BAP=45��+45��=90����
��AB=AP��AB��AP��
�ʴ�Ϊ��AB=AP AB��AP
��2��֤����
��EF=FP��EF��FP
���EPF=45����
��AC��BC��
���CQP=��EPF=45��
��CQ=CP
�� Rt��BCQ��Rt��ACP��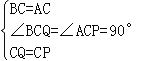
��Rt��BCQ��Rt��ACP ��SAS����
��AP=BQ��
��3��AP=BQ�������������£�
��EF=FP��EF��FP��
���EPF=45����
��AC��BC
���CPQ=��EPF=45��
��CQ=CP
�� Rt��BCQ��Rt��ACP��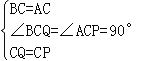
��Rt��BCQ��Rt��ACP ��SAS����
��AP=BQ��