题目内容
【题目】如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD. 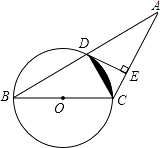
(1)求证:DE为⊙O的切线;
(2)若AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB.又∵∠A=∠B=30°,
∴∠A=∠ODB,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE.
∴DE 为⊙O 的切线
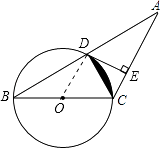
(2)解:∵BC 为直径,
∴∠BDC=90°.
根据等腰三角形的三线合一性质得到CD是AB的中线,
∴BD= ![]() AB=2
AB=2 ![]() ,
,
在直角三角形BDC中,cosB═ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得BC=4,
S阴影=S扇形OCD﹣S△OCD= ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)首先连接OD,根据等边对等角得出∠B=∠ODB,又由等腰三角形ABC的底角为30°,可得∠A=∠ODB,即可证得OD∥AC,继而可证得结论;(2)由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD= ![]() AB=2
AB=2 ![]() ,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.

练习册系列答案
相关题目