题目内容
【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母;
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.

【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)过点C作CD⊥AB的于D,然后以C点为圆心,CD为半径作圆即可;
(2)由切线的性质得∠ADC=90°,利用互余可得∠DCE和∠BCD=的度数,在Rt△BCD中利用∠BCD的余弦可计算出CD的长,然后根据弧长公式求解.
试题解析:(1)如图,
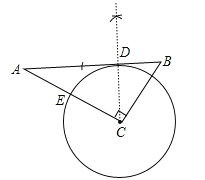
⊙C为所求;
(2)∵⊙C切AB于D,∴CD⊥AB,∴∠ADC=90°,∴∠DCE=90°﹣∠A=90°﹣30°=60°,∴∠BCD=90°﹣∠ACD=30°,在Rt△BCD中,∵cos∠BCD=![]() ,∴CD=3cos30°=
,∴CD=3cos30°=![]() ,∴
,∴![]() 的长=
的长=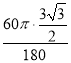 =
=![]() .
.

练习册系列答案
相关题目